Chemical Education Journal (CEJ), Vol. 12, No. 1 /Registration No. 12-2 /Received August 1, 2008.
URL = http://chem.sci.utsunomiya-u.ac.jp/cejrnlE.html

Linear free energy relationships (LFER) as a one hour class-room lecture for post-graduate students: Correlation of the nature of the transition states.

V. Jagannadham^a,

Email: vjchemosmania.ac.in; jagannadham1950yahoo.com

ABSTRACT
Both structure and reactivity are involved in the study of reaction intermediates. The main types of intermediates of interest are carbocations, carbanions, free radicals, and carbenes. Usually, these intermediates are not isolable. Physical organic chemistry is the study of the interrelationships between structure and reactivity in organic molecules. Physical organic chemistry is the study of organic chemistry using methods of physical chemistry such as chemical equilibrium, chemical kinetics, thermochemistry, and quantum chemistry. In the present article an attempt is made to correlate the nature of heterolysis five different free radical type nitroxyl adducts using Hammett's Liner Free Energy Relationships.

Figure & Table
References

A linear correlation exists between the logarithm of a rate constant or equilibrium constant for one series of reactions and the logarithm of the rate constant or equilibrium constant for a related series of reactions respectively. Typical examples of such relations (also known as linear Gibbs energy relations) are the Brønsted relation and the Hammett equation. The name arises because the logarithm of an equilibrium constant (at constant temperature and pressure) is proportional to a standard free energy (Gibbs energy) change, and the logarithm of a rate constant is a linear function of the free energy (Gibbs energy) of activation. It has been suggested that this name should be replaced by linear Gibbs energy relation, but at present there is little sign of acceptance of this change. The area of Physical Organic Chemistry which deals with such relations is commonly referred to as 'Linear Free-Energy Relationships (LFER)'.

Gibbs energy of activation (standard free energy of activation) is DGo the standard Gibbs energy difference between the transition state of a reaction (either an elementary reaction or a stepwise reaction) and the ground state of the reactants. It is calculated from the experimental rate constant k via the conventional form of the absolute rate equation:  DG` = RT [ln (kB / h) - ln (k /T)] where kB is the Boltzmann constant and h the Planck constant (kB/h = 2.08358 × 10¹⁰ K^-1 s^-1). The values of the rate constants, and hence Gibbs energies of activation, depend upon the choice of concentration units (or of the thermodynamic standard state).

Although spontaneous transformations all have negative DGº^o s, not all exergonic processes are spontaneous, due to activation energy barriers to reaction. Treatment of activation energy was framed in terms of enthalpy or potential energy. It should now be clear that, if entropy factors are to be incorporated in the activation barrier, we should be thinking about Free Energy of Activation, DG. The defining equation then becomes:
DG = DH - T DS
Transition state theory proposes an equilibrium between reactants and the transition state, so each of the functions in this equation may be viewed as a [FTransition State - FReactants] difference, where F represents H, S or G. The equations demonstrate the similar exponential relationship of DGºº to Keq and DG to k.

and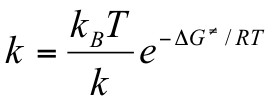

Since the rate constant equation incorporates the temperature variable twice and DG also changes with temperature, observed reaction rates are clearly temperature dependent. Physical Organic Chemists make general use of this relationship in two ways. First, it is a rule-of-thumb that a 10º C increase in reaction temperature will roughly double the rate of that reaction. Second, since this rule applies as well to accompanying reactions, the rates of such side reactions also increase with temperature, sometimes more than the desired reaction. Consequently, the practical yield of the desired product may actually decrease at higher temperatures. Thus, a cleaner (less contaminated) product is often obtained by running a reaction at the lowest effective temperature that gives the desired product. Because DG incorporates a temperature dependent entropy factor and is related exponentially to the rate constant, k, reaction rate studies at different temperatures may be interpreted to provide the activation parameters.

Both the Arrhenius and the Eyring equation describe the temperature dependence of reaction rate. Strictly speaking, the Arrhenius equation can be applied only to gas reactions. The Eyring equation is used in the study of gas, condensed and mixed phase reactions - all places where the simple collision model is not very helpful. The Arrhenius equation is founded on the empirical observation that conducting a reaction at a higher temperature increases the reaction rate. The Eyring equation is a theoretical construct, based on transition state model.

Now let us derive a LFER on the basis of Eyring and Hammett equations: Taking Eyring equation
.........(1)
Taking logarithm
......... (2)
and from Hammett equation

log k = log ko + rs .........(3)

from eqn. 2 and 3
......... (4)
Simplifying and rearranging eqn. 4 one will get
DG = - 2.303RTrs ... (5)
This equation with a particular value of r, applies to any reaction involving a reactant having a series of substituents. For a second series of homologous reactions, with reaction constant r', one can show that
 DG '= - 2.303 RT r's .........(6)
Dividing the equation 5 and 6 by r and r' respectively and subtracting one from the other and on simplification, we get
 DG = (r/r')  DG '+ constant.... (7)
Thus there is a linear relationship between DG of one series and to DG' of another series. Now let us see the application of this relationship to the following putative examples.

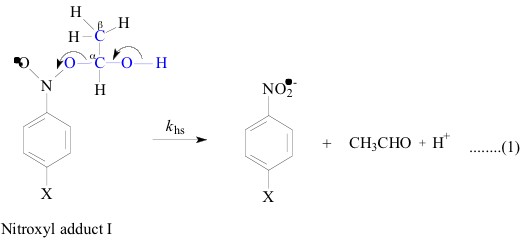
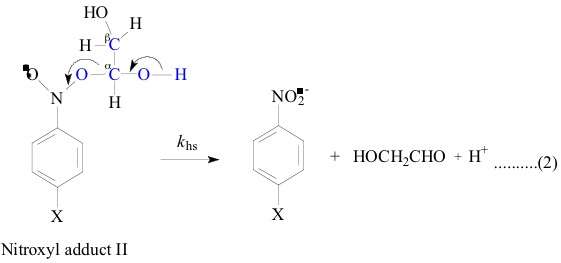
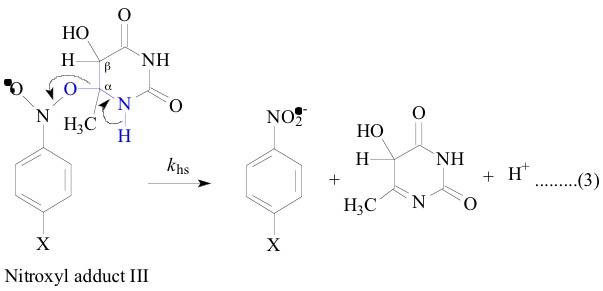
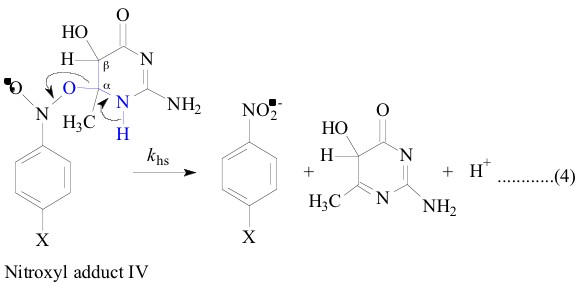
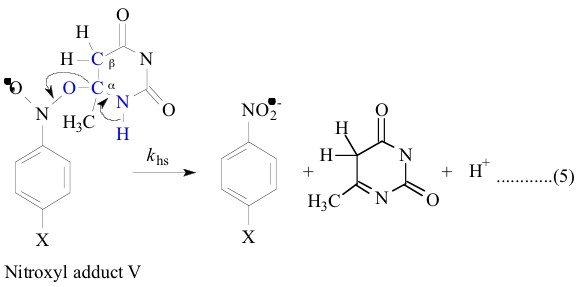
All the nitroxyl adducts I-V were generated [1-4] pulseradiolytically in aqueous solution from nitrobenzenes and the corresponding a-hydroxyethyl, a,b- dihydroxyethyl, 6-methyluracil-6-yl, 6-methyl-i-cytosine-6-yl and 6-methyldihydrouracil-6-yl radicals. Production of a-hydroxyethyl, a,b-dihydroxyethyl, 6-methyluracil-6-yl, 6-methyl-i-cytosine-6-yl and 6-methyldihydrouracil-6-yl radicals were described else where [1-4]. The heterolysis rate constants, khs, and all activation free energy changes were taken from those references. The LFER plot for the heterolysis reaction of the nitroxyl adducts I and V is linear (Figure 1; r = 0.99). The slope of this plot, which should be equal to the ratio of the Hammett ¡ values for the heterolysis of the two, adducts I and V, results as 1.0, in agreement with the individually determined ¡ values (both 1.5). Also the solvent isotope effect (SIE) on khs of adduct V, that is khs(H2O)/ khs(D2O) was found to be 1.7 - 2.3 is similar to that of 2.2 of the adduct I. All these observations led to conclude that the two transition states of the heterolysis of adduct I and adduct V were essentially similar in terms of synchronous O-H and C-O bond breaking assisted by solvent water as shown below. This leads to immobilization of solvent water which was reflected in high negative DS` [1, 4].

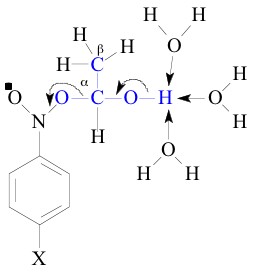and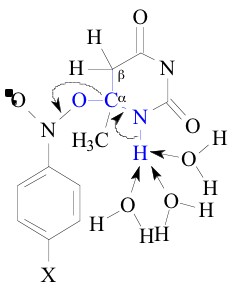

Hence these are all plenty of evidences for the close resemblance of the ±-hydroxyethyl (CH3C.HOH) and 6-methyldihydrouracil-6-yl radicals and which lead to the similar transition states of the adducts on their way to products.

In contrast, the LFER plot for the heterolysis reaction of the nitroxyl adducts III and IV were not perfectly linear when plotted against the nitroxyl adduct I and adduct V (Figure 2, Figure 3, Figure 5 and Figure 6; r = only 0.93, 0.92, 0.95 and 0.91 respectively) which indicates that the ±-hydroxyethyl (CH3C.HOH) is not a good model for the 6-methyluracil-6-yl and 6-methyl-i-cytosine-6-yl radicals. That these belong to a class of their own is shown not only by similar solvent KIE (1.2 - 1.4) which is similar to that of (1.5) observed for the heterolysis of the adduct II but also by the good correlation (Figure 4; r = 0.98) between their own (for the heterolysis of nitroxyl adducts III and IV) corresponding DG` values. To make an attempt to correlate the DG` values of adduct III and IV with that of adduct II, sufficient data for adduct II is not available. Yet the similar solvent KIE is a strong evidence to say that the a,b-dihydroxyethyl radical (HO.CHCH2OH) is a good model for the 6-methyluracil-6-yl and 6-methyl-i-cytosine-6-yl radicals when their adducts, III and IV lead to similar transition states on their way to the products. And adducts II, III and IV differ with adducts I and V where former set have an OH group in b position as shown in their structures above. The strong difference in KIE between the two sets of adducts I, V (1.7 - 2.3) and II, III, IV (1.2 - 1.5) could be understood in terms of the differences in stabilities between the transition states of the two different sets of adducts. The two sets of transition states differ by an OH group in b position to the deprotonatable OH/NH group. Due to the -I effect of OH group in the b position, the adducts II, III and IV are expected to be less stable than the adducts I and V. Besides in the reduction of khs (of C-O bond heterolysis, which is measured in terms of the build up kinetics of the nitro benzene radical anion), this leads to an increased tendency to deprotonate at an early stage of the transition state, i.e. deprotonation tends to precede the heterolysis of C-O bond. This is symbolized as shown below:

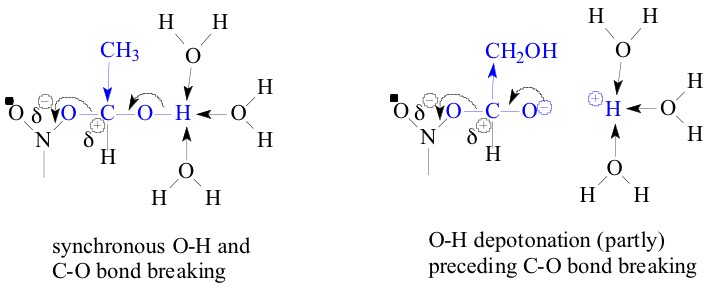
So in conclusion the two sets of adducts (I and V), and (II, III and IV) behave differently and one can conclude that the a-hydroxyethyl radical is a good model for 6-methyldihydrouracil-6-yl radical and a,b-dihydroxyethyl radical is a good model for 6-methyluracil-6-yl and 6-methyl-i-cytosine-6-yl radicals. The structures of the radical anions in the steps 1 - 6 could be read as the following:

Dedication: This article is dedicated to my mentor Prof. Dr. Steen Steenken (Retd), Max-Planck-Institute for Radiation Chemistry, Muelheim a.d. Ruhr, Germany.

References:
[1] Jagannadham, V. and Steenken, S. (1984), J. Am. Chem. Soc. 106: 6542-6551.
[2] Steenken, S. and Jagannadham, V. (1985), J. Am. Chem. Soc. 107: 6818-6826.
[3] Jagannadham, V. and Steenken, S. (1988), J. Phys. Chem. 92: 111-118.
[4] Jagannadham, V. and Steenken, S. (1988), J. Am. Chem. Soc. 110: 2188-2192.