Chemical Education Journal (CEJ),
Vol. 12, No. 1 /Registration No. 12-4/Received October 20, 2008.
URL = http://chem.sci.utsunomiya-u.ac.jp/cejrnlE.html
Abstract
The intention of this work is to present a visual method which
serves to obtain the characters of irreducible representations
(CIR) and symmetry types of point group D3h.
The used method is based on transformations of geometrical figures,
which have the same symmetrical operations as a given molecule.
The problems - which constitute one of the subjects of Molecular
Spectroscopy explorations with Group Theory application
- require, in this approach, only elementary calculus and simple
geometry and seems to be convenient for introductory chemistry
and physics. The authors prepared software and computer simulations
in order to show the simplicity of the method. These teaching
aids are presented and described in this paper. The elaboration
also contains the mathematical insight into the applied method.
There are calculated active vibrations and frequencies for the
D3h group, too. Results are strictly related
to the geometrical model.
I. INTRODUCTION
II. COMPUTER SIMULATIONS AND SOFTWARE
III. CHARACTERS OF IRREDUCIBLE REPRESENTATIONS
IV. MATHEMATICAL INSIGHT OF THE
APPLIED METHOD.
V. SUMMARY
VI. REFERENCE
Atomic cores in a molecule oscillate around a position of equilibrium.
These complicated motions can be decomposed into components receiving
normal vibrations, which are often used in Molecular Physics
by Group Theory to determine - among other things - dislocation
and amplitudes of nuclei in a molecule. The aforementioned Theory
applies symmetry operations to a given molecule to determine CIR
and simultaneously, kind of oscillation, whose effects are visible
(if active) on a screen as a form of a spectrum. Symmetry is essential
for our consideration too. There exists the definition of symmetry
given by Weyl1 and contained
in "The Feynman Lectures of Physics"2
as well as equivalent definition which refers to the symmetry
operation. It says: "The symmetry operation to a molecule
is such a transformation, as a result of which the particle takes
a new position indistinguishable from the initial one."3 The definition is adopted for
exploring vibrations of flat molecules which belong to D3h point group like, for instance, SO3
and ion NO3-. The point group
is realized by a set of all symmetry operations to a given molecule
and an action which relies on composing (i.e. making in turn)
the operations. But instead of exploring directly a molecule,
we use a method which is - previously used for C2v
and C4v point groups3
- applied to a geometrical figure which has the same symmetry
operations as a given molecule. The shape of the figure corresponds
to the shape of the potential well created by the molecule's atomic
cores. The authors expanded the method on the D3h
group. Transforming the figure through all symmetry operations
enable us to obtain CIR and the type of vibration in a very simple
and elegant way. Furthermore these methods seem to be transparent
and comprehensible, especially applicable for introductory chemistry
and physics courses at university. The paper is organized as follows:
Section II. presents software and computer simulations of the
discussed molecule's oscillations, as well as transformations
of some figures which symmetry operations correspond with the
ones of a given molecule.
Animations and software are available at <www.matphys.kki.pl>
(also see Ref.4)
Section III. deals with finding CIR on geometrical figure transformations
through symmetry operations.
Section IV. gives mathematical insight of applied method as well
as calculations of active vibrations and frequencies in IR.
II. COMPUTER SIMULATIONS AND SOFTWARE
There is no other better way to attract someone's attention and make him (or her) interested in presented topic than visualization and possibility of interactive work within a considered problem. Therefore the authors created a number of computer simulations (animations) and software4 to give the reader an opportunity of elaborating the topic by him or herself. Basically, there are two groups of animations - the first one uses a simple geometrical figure and its transformations through all symmetry operations which are assigned to a given molecule. There is a chance to discover CIR by just conversing the figure and observing results. It is possible to open the simulations in most of Media Players. Figures are mostly coloured to draw attention and minimize any mistakes during observation. Results serve as data for software.
The second group constitutes stereo forms of molecules together with their oscillations what enables to observe deflections of the atoms of molecules and simultaneously notice directions of their dislocations. In addition, there exists the opportunity to predict, whether or not, a vibration is active in IR. In other words, whether it is observable as a spectrum, and if so, what kind of spectrum that would be - parallel or perpendicular bands. Animated oscillations are arranged in types and are compatible to software results.
The software uses symmetry operations and found - through application of simulations - characters of irreducible representations, to get the number and symmetry type of a given oscillation ( more details on symmetry type you can find at < www.matphys.kki.pl >). Symmetry operations - necessary for the program - are subject to be found either by using the examined molecule or geometrical figure to which it corresponds.
Adopted conditions for the program are standard ones. This means that the lengths of bonds were measured at determined (standard) temperature and pressure.
III. CHARACTERS OF IRREDUCIBLE REPRESENTATIONS
It is well known that CIR enables one to determine the type of oscillations of a given molecule. The approach here is based on applying a geometrical figures which have the same symmetry operations as an examined molecule. The figure which is taken for finding irreducible representations, reflects the atomic cores of a molecule and illustrates an energetic level. Applied signs (+), (-), describe the quantum state of a molecule. They constitute the representation of a wave function. Symmetry, which often constitutes the connector between physical laws,5 is here the basis for understanding various kinds of molecular spectra. The outline of the first figure is used and remains unchangeable for the next ones. Alterations may occur as division of the first figure. The reader can find the similar approach in Siegel's article,6 where the discussed field of exploration was described by a strict geometrical display. This way allows one to find all CIR of considered molecules. Explorations are oriented on D3h point group and molecules which belong to it like NO3- and SO3.
An equilateral triangle is used as a figure to be transformed because it has the same shape as the molecule. Symmetry operations, which can be assigned to both NO3-(SO3) and the equilateral triangle are as follows: E, 2C3, 3C2, sh, 2S3, 3sv. For more details see Ref.7
In order to get CIR of A1' symmetry type we take aforementioned triangle to all symmetry operations. We use triangle's outline for transformations. In computer simulations, the triangle is coloured, for better visualization. No matter how one transforms the triangle one gets the same shape (Fig. 1(a)).
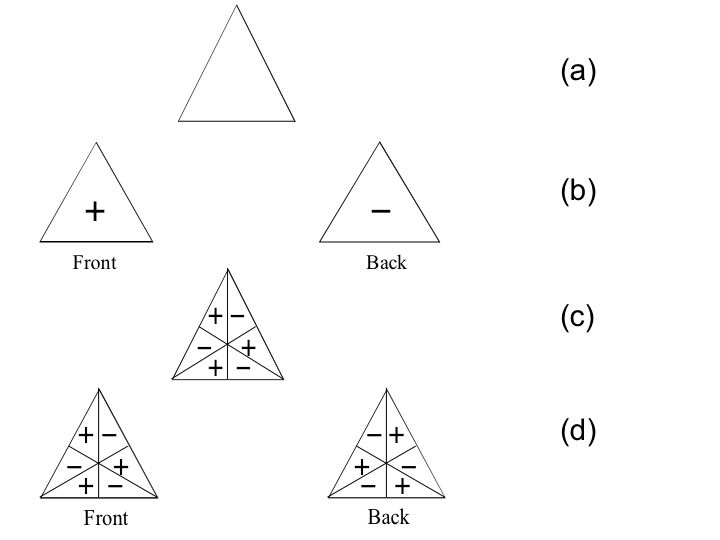
Fig.1. Figures which serve to obtain CIR of non-degenerated
vibrations:
(a)it serves to obtain A1' symmetry type
(b)two plane - sites of the same figure (2 subfigures) enable
one
to obtain A2'' type
(c)triangle is divided by its heights and this gives us A2'
(d)two subfigures of the same triangle but with opposite signs
on both its plane - sites. It serves to obtain A1''
type
If a figure comes into itself (after accomplishing an operation),
then we ascribe it 1. Conversely if a figure is passing into the
opposite one as a result of the sign's change, then we ascribe
it -1. Hence, one receives A1' symmetry
type (Table 1).4
In Fig. 1(b) we have the same triangle
but with different signs on each plane-site. Additionally, there
is no division of the triangle's side. This figure gives us A2" symmetry type (Table
1), which is visible in the spectrum as a parallel band.4
| E | 2C3 | 3C2 | sh | 2S3 | 3sv | |
| A1' | 1 | 1 | 1 | 1 | 1 | 1 |
| A1'' | 1 | 1 | 1 | -1 | -1 | -1 |
| A2' | 1 | 1 | -1 | 1 | 1 | - 1 |
| A2'' | 1 | 1 | -1 | -1 | -1 | 1 |
| E' | 2 | -1 | 0 | 2 | -1 | 0 |
| E" | 2 | -1 | 0 | -2 | 1 | 0 |
A new form of the triangle is shown in Fig. 1(c). The triangle's heights divide each its sides into two parts. The front sign corresponds to the rear one. Transformations give A2' symmetry type (Table 1), of inactive vibrations.4
In Fig. 1(d) we have the same figure as at A2' but with opposite signs on both triangle's plane - sites. If we make transformations then we obtain CIR of A1'' symmetry type.
B. Degenerated vibrations
Let us divide an equilateral triangle into two equal parts. As a result we obtain two right triangles. There are 3 ways in which such a triangle can be obtained depending on which one of the triangle's heights we choose. Therefore, we may obtain either a or b or c (Fig. 2(i)) or if the triangle is reflected with respect to the horizontal axis then we obtain r, s, t (Fig. 2(i)). The only assumption is that we reflect the first triangle a receiving r, and the successive triangles s and t we receive as a result of revolution of the triangle r at 120° and 240° the counterclockwise direction with respect to the axis which is perpendicular to the triangle's plane and passes through its center. In this way, one obtains two groups of triangles a, b, c and r, s, t from which each next one is turned by 120° with respect to the previous one. One may perform the reflection triangle a onto r not necessarily with respect to horizontal axis but an arbitrary one which is parallel to any triangle's side. We choose one triangle from each group e.g. a and r, but equally we may choose any other two triangles. These are so called Introductory Figures (IF). They receive numbers which are twice as high as numbers due to figures obtained as a result of transformation (Eq. 1). Next, we make transformations due to symmetry operation of NO3-(SO3). Each IF is transformed separately and numerical results are added. We ascribe numbers as follows: IF are ascribed with the number 1, their oppositions (marked by "prim") or figures of opposite signs on each triangle's plane - sites are ascribed to -1. The other figures are ascribed to -1/2 and their oppositions (marked by "prim") 1/2 (Eq. 1). Figures receive the above numbers after accomplishing an operation. For instance, we want to find character for C3. If our IF are a and r then revolution a by 120° gives b which receives number -1/2 and revolution r at the same angle gives s which receives the -1/2. We add up the numbers and receive -1 or the number which is character for C3.
Fig.2. Figures which serve to obtain degenerated triangles:
(i)two groups of triangles (a, b, c) and (r ,s, t) which enable
E' type to be found.
(ii)the same two groups as at (i) but with a different sign on
each surface
of the same triangle. It serves to obtain CIR of E" symmetry
type.
In case of operation C2 and sv we make not one but 3 transformations of each IF due to their being 3 axes (C2) and 3 planes of reflection (sv). We add up results of the transformations separately in each group and then add up results of both groups. For instance, we want to receive a character for C2. Let us assume a and r as IF. We transform a with respect to the axis which contains the triangle's height and passes through its bottom side. The result is a' which is ascribed with number -1. Then, we transform a with respect to successive axis, for example, the one which contains the triangle's height and passes through its left side. The result is b' which receives 1/2 according to Eq. 1. Lastly figure a is transformed with respect to the third axis which brings it to c' and number 1/2. We add up the numbers receiving 0. We do the same with the second IF or r. The result in the second group is 0. Finally, we add up the results of both groups of C2 operation which receives 0 or CIR. All the above brings us to the possibility of obtaining CIR for E' symmetry type (Table 1) which gives doubled degenerated oscillations of perpendicular bands spectrum, available at simulations.4
Fig. 2(ii) presents the same two groups of triangle as those serving to find E' but with a different sign on each surface of the same triangle. Analogically we can obtain E" symmetry type. The only difference is at 3C2 and 3sv where we subtract the results received in each group. All types discovered show strict compatibility with those of Carter,8 which joins molecular symmetry with group theory, and the elaboration by Cornwell.9
IV. MATHEMATICAL INSIGHT
OF THE APPLIED METHOD.
ACTIVE VIBRATIONS IN IR.
A. The mathematical inspection:
We place the NO3-(SO3)
molecule in plane XY (Fig. 3)
The matrices simultaneously represent the described transformation of an arbitrary point on the plane as follows:
.jpg)
For rotations C2 and reflections sv, we have 3 transformations - with respect to each axis (plane) presented in Fig. 3. Each axis is rotated with respect to the previous one by about 120°. Therefore by rotating C2 with respect to axis 1, by about 180°, with respect to axis 2 about 180°+120°=300°, and with respect to axis 3 about 180°+240°=420° we find the following result:
.jpg)
The numbers within matrices correspond to the ones which have
been assigned to the result of transformation of geometrical figure.
Let us take into account e.g. E' symmetry type. Each number
on the main diagonal is assigned to the result of the transformation
of IF. These numbers should be added together so as to obtain
the character. For example, revolution C3
of the first IF e.g. a (Fig.
2(i)) about 120° brings it to b. This result is
assigned as -1/2, according to Eq. (1),
which corresponds to the first number on the main diagonal of
matrix M(C3). The revolution about 120°
of the second IF i.e. r brings it to s, which is
assigned as -1/2 Eq. (1). This corresponds
to the second number on the main diagonal of M(C3).
When we add up these numbers we receive the result: CIR: (-1/2)
+ (-1/2) = -1. A similar approach applies to other matrices except
C2 and sv where
one needs to perform three operations with respect to each axis
(plane) separately. The results cover the numbers on the main
diagonals of M(C2'), M(C2"),
M(C2"'). We add up the obtained numbers
of the first group (Fig. 2(i)) and
then the second group. Finally, we add together the results of
both groups.
See appendix, in order to get correlations between numbers in
matrices (2), (3) and the numbers which are assigned to the results
of geometrical figurers' transformations.
B. Active vibrations and their frequencies
There exists a well known formula in Molecular Spectroscopy:
which allows one to calculate the number of translations, rotations
and oscillations of a determined symmetry type. The meaning of
the consecutive symbols is as follows:
h - number of all symmetry operations
in the point group,
hq - number
of symmetry operations in qth class, where class
is a set of
symmetry operations which have the same characters. E.g. if we
take
into account NO3, then the class 3C2 means two proper rotations,
cq(I)
- character of irreducible representation of the qth
class (see Table 1),
cq(R)
- character of reducible representation of the qth class.
More
informations on the character of the reducible representation
at
< www.matphys.kki.pl
> ,
K - symmetry type.
One may find more details expanding on how to find these quantities in Kecki's book on elements of molecular spectroscopy.10 But, because the considerations in this paper are oriented on oscillations only, and in addition, active in IR, the Eq. (4) has been modified in such as way to eliminate translations and rotations and receive only oscillations. Therefore one obtains:
where c denotes the number of translations and rotations of a given symmetry type. It turns out that c for vibrations active in IR and for Dnh point groups - which the authors deal with in this paper - remains constant and equal 1. This is easy to verify by applying known methods. Therefore, for NO3- (SO3) one receives: N (A2") = 1, N (E') = 2, or equivalently:
N IR osc = A2" + 2E' (6)
where, N IR osc denotes the total number of oscillations in IR. The modification Eq. (4) into (5) allows one to get direct results, which also could be found by examination, step by step, translations and rotations.12 Both ways lead to compatible results.
One may achieve the description of vibrations applying inner coordinates (further denoted h). These coordinates refer to the change of the bond lengths and angles between them.The number of inner coordinates overlaps the number of degrees of freedom which is 3n - 6 for polyatomic molecules. In case of D3h molecules there are 6 inner coordinates. The way of vibrations calculation is based on Lagrange equation (7)
.jpg)
where i = 1, 2, 6 for molecules which belong to D3h group. The potential energy expression in
harmonic approximation is given by Eq.
(8)
In order to determine kinetic energy (T) one needs to know kinetic coefficients aij which are made on the base of known atomic masses, bond lengths and angles between them. Then kinetic energy is given by the Eq. (9)
The forms of potential (8) and kinetic (9) energies give us the possibility to resolve Eq. 7 and obtain a set of equations (10)
| SO3 | NO3 | ||
|---|---|---|---|
| symmetric stretching | 1065 | symmetric stretching | 1050 |
| degenerate deformation | 530 | antisymmetric degenerate (I) | 720 |
| degenerate stretching | 1391 | antisymmetric degenerate (II) | 1360 |
| symmetric deformation | 498 | ||
which enables one to find 6 unknowns w2 in D3h molecule and simultaneously 6 frequencies (n) of vibrations because w= 2pn. The condition to resolve (10) is that the determinant (11) must be zero.
The conducted calculations for molecule SO3 and ion NO3- give the results which are gathered in Table 2. The results are compatible with experiments, presented by Cabannes11 and also recommended by Lide12. Fig. 4. presents sample pictorial spectrum of SO3, where 1/l1 refers to symmetric deformation vibration, 1/l2 - degenerate deformation, 1/l3 - symmetric stretch, 1/l4 - degenerate stretch vibration, respectively
Fig.4. Pictorial spectrum of SO3
V. SUMMARY
This paper has discussed the method of finding the character
of irreducible representations - which are widely applied by Molecular
Spectroscopy - based on symmetry correlation between a molecule
and it's corresponding figure. Associated with the topic Group
Theory is a powerful instrument for facilitating and enabling
calculations. Some parts of the Theory - which require
certain mathematical apparatuses - have been simplified in such
a way that transformations of figures can be considered, and thereby,
to find CIR necessary to get the types and number of vibrations.
The modified way of calculating active vibrations in IR connected
with previously found CIR has been described. In addition, there
have been also calculated frequencies of vibrations of NO3- and SO3.
Such an approach gives the student the opportunity to become more
familiar with the theme. The presented method could be applicable
to theoretical physics teaching integrating problem simulation.
That there is a possibility of using simulations and software
means that one could consider introducing the enriched material
at university level. For greater
clarity on Molecular Spectroscopy, we suggest Ref. 13. and for Group
Theory we suggest Refs. 9
and 14. The authors concentrated
on point groups D3h but the considerations
could easily be expanded to other groups and molecules.
ACKOWLEDGMENTS
The authors wish to thank prof. W. Nawrocik and prof. H. Szydlowski from the Institute of Physics ( Adam Mickiewicz University ) for some significant suggestions on symmetry and computer simulations.
APPENDIX
1. E" symmetry type
This type of symmetry corresponds to the same figures
as those for E' but with a different sign on each surface of the
same triangle (Fig.2(ii)). The change
of the sign occurs only at the reflection with respect to the
plane which contains a molecule, or sh, S3, S32.
Therefore, the matrix representations for E" symmetry are
the same as those for E', except for the aforementioned sh, S3, S32,
where we have opposite numbers on the main diagonal. The numbers
which are on the main diagonal correspond to those at Eq. (1).
In other words, they are the numbers assigned to the result of
each transformation.
-2.jpg)
2. A1' symmetry type
In order to get the characters for this type of symmetry
we calculate the determinants of matrices presented for E' and
E". They simultaneously constitute the numbers assigned to
the result of each symmetry operation for Fig.1(a).
3. A2" symmetry
type
This type corresponds to the same figure as for A1' but
with the opposite signs on each surface of the same triangle Fig.1(b). This means that the characters
should be determined with the opposite number for operations which
cause the change of the sign at the triangle's transformations.
These are: sh,
S3, S32
and 3C2. The resulting numbers are those
which serve to determine CIR for this type.
4. A1" symmetry
type
We establish the characters corresponding to a change
of sign at the deflection point along Z axis. In other
words, we observe an alteration at coordinate z. In addition,
we use the condition of vectors orthogonality along vertical columns
in the table of characters. The established numbers correspond
to those ones assigned to the results of consecutive operations
for Fig.1.(d).
5. A2' symmetry
type
We take the same figure (Fig.1(c))
as for A1" type but with the same
sign on both planes/sides of the same triangle. Therefore the
operations which change a sign into an opposing one receive opposite
numbers. Those operations are: sh, S3, S32
and 3C2. This is in accordance with the
process described in the previous text (Sec.
III (A)).
1H. Weyl, Symmetry, (Princeton University Press, New Jersey, 1983), Chap. 1, pp.4 - 5. and Chap.2 , pp. 41 - 42.
2R. P. Feynman, R. B. Leighton, M. Sands, The Feynman Lectures on Physics, (Addison - Wesley, Reading, MA, 1963), Vol. 1, Chap. 11, p. 168.
3P. Kowalczyk, Physics of Molecules, (PWN SA, Warsaw, 2000), Chap. 1, p. 12 and pp. 35 - 44.
4Computer simulations and software are available at < www.matphys.kki.pl>. You can writedown the address in the line of addresses: http// of Internet Explorer or in other searching areas, for example "Google".
5J. Hanc, S. Tuleja and M. Hancova, "Symmetries and conservation laws: Consequences of Noether's theorem," Am. J. Phys., 72 (4), 428 - 433 (2004).
6D. Siegel, "Cinematographic metaphors for the relativistic revolution," Am. J. Phys., 74 (3), 173- 174 (2006).
7H. Haken and H. C. Wolf, Molecular Physics and Elements of Quantum, (PWN SA, Warsaw, 1998), pp. 112 - 138.
8R. L. Carter, Molecular Symmetry and Group Theory, (J. Wiley and Sons, N.York, 1997), p. 266 and p. 267.
9J. F. Cornwell, Group Theory in Physics, (Academic Press, London, 1984), p. 333 and p. 329.
10Z. Kecki, Elements of Molecular Spectroscopy, (PWN SA, Warsaw, 1998), Chap. 3, pp. 110 -114.
11J.Cabannes, "Spectroscopy applied to molecular physics", Reports on Progress in Physics, 10 (1), p. 412 (1944).
12D.R. Lide, Handbook of Chemistry and Physics, (CRC Press, London, N.York, Washington 2004), Chap. 9, p. 78.
13Gordon M. Barrow, Introduction to Molecular Spectroscopy, (McGraw-Hill, New York, 1962), pp. 141 - 197.
14S. B. Piepho and
P. N. Schatz, Group Theory in Spectroscopy: with applications
to magnetic circular dichroism, (J. Wiley & Sons, New
York, 1983), pp. 161 - 200.