Chemical Education Journal (CEJ),
Vol. 12, No. 1 /Registration No. 12-1/Received July 5, 2008.
URL = http://chem.sci.utsunomiya-u.ac.jp/cejrnlE.html
Keywords: Three-dimensional models, Polifacil system, drinking straws, molecular geometry, misconceptions on spatial geometry.
Abstract (In English)
A simple system for building three-dimensional models of polyhedra
made of drinking straws and raffia, named Polifacil,a
is presented. It is an inexpensive and very suitable tool for
being used by children in the learning of the spatial geometry
or by undergraduate and graduate chemistry students in the learning
of the molecular geometry and group theory. The procedure for
building three sets of models is given: a) The trigonal, square,
pentagonal and hexagonal pyramids; b) The tetrahedron, trigonal
bipyramid, octahedron, square and pentagonal antiprisms; c) The
trigonal dodecahedron, monocapped pentagonal antiprism and icosahedron.
The discovery of undergraduate chemistry students' misconceptions on the geometry of usual polyhedra has prompted us to divulgate this system as workshops for children in our "National Weeks of Science and Technology".
Abstract (En este resumen
se suprimieron los acentos y los caracteres especiales para mejorar
su presentacion en la web)
Se presenta un sistema sencillo, llamado Polifacil, de
construccion de modelos tridimensionales de poliedros hechos con
popotes y rafia. Es una herramienta economica y muy apropiada
para usarse con los ninos en el aprendizaje de la geometria
del espacio o por los estudiantes de quimica de licenciatura y
de posgrado en el aprendizaje de la geometria molecular
y la teoria de grupos. Se proporciona el procedimiento para la
construccion de tres series de modelos: a) Las piramides
trigonal, cuadrada, pentagonal y hexagonal; b) El tetraedro, la
bipiramide trigonal, el octaedro y los antiprismas cuadrado y
pentagonal; c) El dodecaedro trigonal, el antiprisma pentagonal
monoapuntado y el icosaedro.
El descubrimiento de ideas erroneas en muchos de nuestros estudiantes de licenciatura en quimica, respecto a la geometria de poliedros comunes, nos impulso a divulgar este sistema en forma de talleres para ninos, en nuestras "Semanas Nacionales de Ciencia y Tecnologia".
Contents.
i) Abstract (In English).
ii) Abstract (In Spanish).
I Introduction.
I.1 Undergraduate chemistry students'
misconceptions on spatial geometry.
I.2 The origin of "Polifacil
system".
II Construction of 3D models by using
Polifacil.
II.1 Construction of trigonal, square,
pentagonal and hexagonal pyramids.
II.1.1 Construction, in steps, of a
trigonal pyramid.
II.1.2 General procedure for making
square, pentagonal and hexagonal pyramids.
II.2 Construction of polyhedra derived
from chains of equilateral triangles: Tetrahedron, trigonal bipyramid,
octahedron and square and pentagonal antiprisms.
II.3 General procedure for the building
of polyhedra derived from a square and pentagonal antiprisms:
Trigonal dodecahedron, monocapped pentagonal antiprism and icosahedron.
II.3.1 Construction of a trigonal dodecahedron.
II.3.2 Construction of a monocapped
pentagonal antiprism and an icosahedron.
III Application of the Polifacil
models in the teaching and learning of the geometry of polyhedral
molecules.
IV Conclusion.
V Notes and references.
I Introduction.
I.1 Undergraduate chemistry
students' misconceptions on spatial geometry.
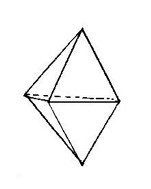
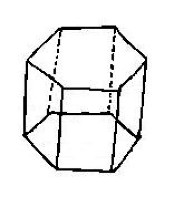
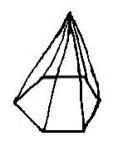
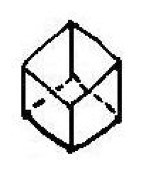
Although geometry is a very important tool in several
fields of science, we have found that in our university many of
high school and undergraduate students do not have a clear understanding
of the basic concepts of spatial geometry. For example, the application
of some diagnostic tests at the beginning of an inorganic or organic
stereochemistry courses revealed that our undergraduate chemistry
students do not match the name of the usual polyhedra with their
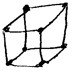
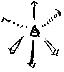
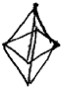
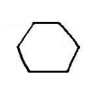
physical forms. Thus, instead of the tetrahedron, the octahedron
and the hexahedron they provided drawings of some polyhedra different
to those required and, surprisingly, also... "Polygons!"
(Tables 1 - 3: Arroyo-Carmona, 2005;
Perez-Benitez, 2008).
 |
 |
 |
 |
   |
|||
 |
 |
 |
 |
  |
|||
 |
 |
 |
 |
 |
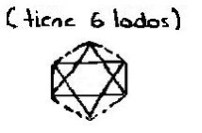 |
I.2 The origin of "Polifacil"
system.
Bearing in mind the problem mentioned above, we have developed
a simple system for building 3D models of polyhedra and we have
divulgated it as workshops in scientific chemical meetings (Pérez-Benítez, 1991)
and also in our "National Weeks of Science and Technology"
for children and their parents. This system was derived from the
invention of the Finland artist Astrid Gröndlund, who built
a geometrical mobile for children's room, made of octahedra. Each
octahedron was constructed inserting a thin copper wire into 12
straws arranged as a chain of triangles (Borglund,
1972; Figure 1).
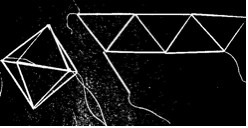
Looking for other starting materials, we found that drinking straws and raffia (a commercial plastic ribbon) are well suited: They are resistant enough, accessible, manageable and inexpensive in creating several colorful and lasting 3D models of polyhedra. Thus, they are quite appropriate for the teaching and learning of the geometry of usual polyhedra, from basic to advanced educational levels.
The most important advantage of this system (which we named in Spanish "Polifacil" and means "easy polyhedra") is that, starting from a 2D structure, the angles are automatically determined when the polyhedron is formed. This is strictly true when all of the polyhedron's faces are triangles; but in contrast, when it is shaped only with faces different to 3-side polygons, the resulting polyhedron is unstable, such as in the case of the cube. In the middle are polyhedrons whose topicity is a combination of triangles and other higher polygons, as in the case of square antiprism that is composed of 8 triangular and 2 square faces.
To illustrate the above mentioned, in this article is presented
the construction of three sets of models:
1) Pyramids: Trigonal, square, pentagonal and hexagonal pyramids.
2) Polyhedra derived from a chain of equilateral triangles: Tetrahedron
(Pérez-Benítez, 1991:
pp. 198-200), trigonal bipyramid, octahedron, square and pentagonal
antiprisms.
3) Polyhedra derived from square and pentagonal antiprisms: Trigonal
dodecahedron, mono- and bicapped pentagonal (icosahedron) antiprisms.
II The construction of 3D models.
II.1. Trigonal, square, pentagonal
and hexagonal pyramids.
Materials:
a) Twenty red drinking straws of 5 cm.
b) Eighteen blue drinking straws of 8 cm.
c) Four pieces of raffiab
of 1 m long.
II.1.1 Construction, in steps,
of a trigonal pyramid.
1) Insert the raffia into three red straws and tie it firmly
to form the trigonal pyramid's bottom (Figure 2a-b). One end of
the raffia should be left short (SE) and the other large
one (LE) (Figure 2b)c.
2) Insert the LE into two blue drinking straws and pass
it by the inner part of the triangle at the point 2 (Figure 2c).
3) Pull it firmly and then make a simple knot as it is illustrated
in Figure 2d.
4) Insert the LE by the inside of the straw 2-3 and make
a simple knot at the point 3 (Figure 2e). It is necessary to make
a knot at each vertex that the LE arrives; if it is not
well done the polyhedron losses rigidity.
5) Insert the LE into one blue straw (Figure 2f) and tie
it by joining the point 4 with the apex 5 (Figure 2g).
6) Cut the remaining raffia of the LE or retain it if you
wish to hang the polyhedron.
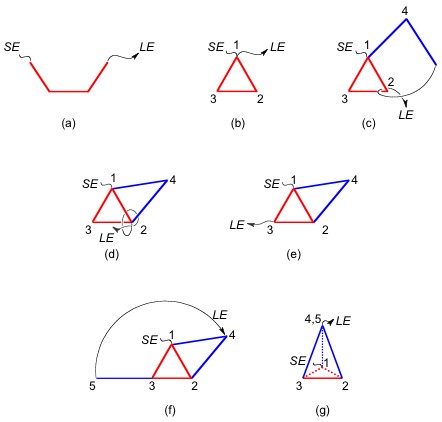
II.1.2 General procedure for
making square, pentagonal and hexagonal pyramids.
The extend structures for building these pyramids are illustrated
on the left of the Figure 3. They can be constructed as follows:
After the elaboration of the pyramids' bottoms with four, five
or six red straws, followed by the insertion of two blue straws
for the construction of their first triangles on the edges 1-2,
the LEs must be inserted inside of the straws 2-3 and tied
it at their vertices number 3. Then, a couple of blue straws have
to be added for constructing the second triangle and the LEs
are tied at vertices number 4.
In the case of square pyramid, the LE is going back to the vertex number 6 and tied with the vertex number 5 to conclude the model (Figure 3a right), while in the case of pentagonal and hexagonal pyramids their LEs must be inserted into the straws 4-5 and tied them at the vertices number 5. Then, one or two blue straws have to be added and joined to the vertex number 6 and 7 to conclude the pentagonal pyramid (Figure 3b right) or the LE has to be tied at the vertex 6 for making the third triangle of the hexagonal pyramid (Figure 3c left). Then, the LE is going back to the vertex number 9 and joined with the vertices number 7 and 8 to conclude the model (Figure 3c right). The terminated models are presented in Figure 4.
II.2 Construction of polyhedra
derived from chains of equilateral triangles: Tetrahedron, trigonal
bipyramid, octahedron and square and pentagonal antiprisms.
All of these models can be constructed from their extended
structures which are chains of two, four, five, seven and nine
equilateral triangles (Figure 5 left). With exception of the trigonal
bipyramid, one straw must be added after the construction of those
chains of triangles.
Note that we use only straws of the same size (red color code)
for building these models even if the length of the straws can
be conveniently changed for increasing or decreasing the height
of the trigonal bipyramid and the square and pentagonal antiprisms
(Figures 5d, 5h and 5j). The reason of this fact is that the construction
of trigonal dodecahedron and icosahedron (other regular polyhedron)
is based on the square and pentagonal antiprisms (see next section).
Even though this time the detailed instructions for building these
models are not provided to avoid repetitions (compare for example
the extended structure of trigonal pyramid (Figure
2f) with that of tetrahedron (Figure 5a)), we have noted that
some children have difficulties to make, for example, the trigonal
bipyramid, because they carry out the step illustrated in the
Figure 2e instead of introducing two straws to make the triangle
2,5,4 of the trigonal bipyramid's extended structure (Figure 5c).
So, be sure of following the sequence: three straws - knot - two
straws -knot - two straws - knot, etc., which gives rise to: first
triangle - second triangle - third triangle, etc.
The terminated models are presented in Figure
6.
Materials:
a) 43 red drinking straws of 5 cm.
b) 5 pieces of raffia of 1 m long.
II.3 General procedure for
building polyhedra derived from the square and pentagonal antiprisms:
Trigonal dodecahedron, monocapped pentagonal antiprism and icosahedron.
Even thought trigonal dodecahedron and icosahedron
can be constructed by closing their respective extended structures
(not showed here), we have found that their construction is more
understandable if they are built in steps, being the first one
the construction of the square and pentagonal antiprisms (see
above).
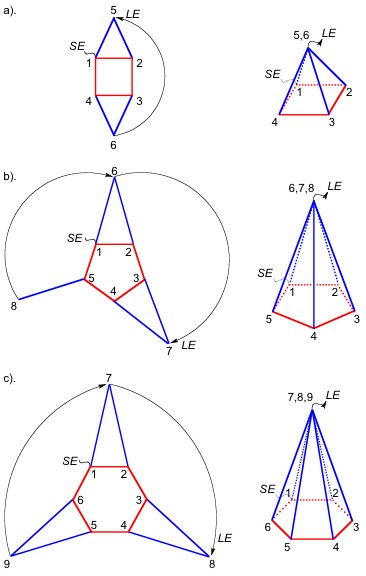
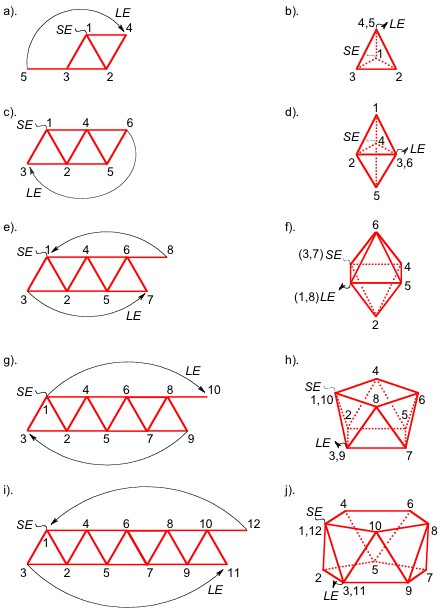
In fact, other advantage of this system is that a polyhedron can be modified very easily. For example, the square antiprism can be converted in a trigonal dodecahedron if their square faces are transformed in triangles by the addition of one straw in each face; thus, the blue and green lines of the Figure 7 accomplish this purpose.
In the same way, the pentagonal antiprism is converted in an icosahedron if their two pentagonal faces are capped, which signifies that the two pentagonal faces have to be transformed into pentagonal pyramids, following the procedure described in the section II.1.2 (Note the resemblance among the Figures 3b and 8a). The semi-extended structure for building the monocapped pentagonal antiprism is presented in the Figure 8a, while the Figure 8c schematizes the semi-extended structure for making the bicapped pentagonal antiprism or icosahedron (Figure 8d).
The added straws (green and blue) for building these three models (sections II.3.1-2; Figures 7 and 8) are of different color than the initial polyhedron (red) only for didactical purposes but all of them must be of the same size. The terminated models are presented in Figure 9.
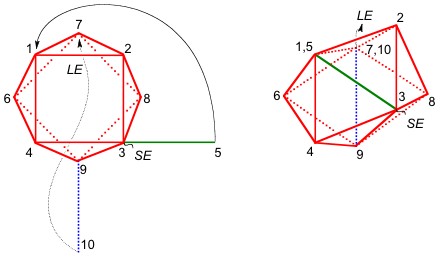
II.3.1
Construction of a trigonal dodecahedron.
Materials:
a) The square antiprism built in the section II.2 (Figure
5g-h).
b) 1 green drinking straw of 5 cm.
c) 1 blue drinking straw of 5 cm.
d) 0.5 m of raffia.
II.3.2 Construction of a monocapped
pentagonal antiprism and icosahedron.
Materials:
a) The pentagonal antiprism built in the section II.2 (Figure 5i-j).
b) 5 green drinking straws of 5 cm.
c) 5 blue drinking straws of 5 cm.
d) 1 m of raffia.
III Application of the Polifacil
models in the teaching and learning of the geometry of polyhedral
molecules.
We had been using these models in our inorganic stereochemistry
courses (Figure 10a) for the teaching and learning of the geometry
of polyhedral molecules such as those described in the table 4.
In the case of molecules which posses a central atom, the Polifacil
models can be conveniently adapted simply by tying pieces
of raffia from the vertices to the center of the polyhedron and
modeling balls of plasticine at its sites and with the colors
you consider necessary (Figure 10b).
At this point is very useful to introduce the IUPAC's nomenclature of the polyhedra which are used often for the representation of chemical structures you could be dealing in a class. It is also possible to include other topics related with the molecular structure such as the Valence Shell Electron Pair Repulsion Theory (VSEPR) and Coordination Chemistry.
|
|
|
| Polyhedron | IUPAC symbol | Symmetry point group | Related chemical structure |
| Trigonal pyramid | TPY-3 | C3v | NH3 |
| Square pyramid | SPY-5 | C4v | BrF5 |
| Pentagonal pyramid | PPY-6 | C5v | XF6 |
| Hexagonal pyramid | HPY-7* | C6v | MoF82- |
| Tetrahedron | T-4 | Td | CH4 |
| Trigonal bipyramid | TBPY-5 | D3h | PCl5 |
| Octahedron | OC-6 | Oh | SF6 |
| Square antiprism | SAPR-8 | D4d | ZrF82- |
| Pentagonal antiprism | PAPR-10 | D5d | Fe(C5H5)2 (staggered) |
| Trigonal dodecahedron | DD-8 | D2d | Mo(CN)84- |
| Monocapped pentagonal antiprism | PPRP-11 | C5v | B11H112- |
| Icosahedron | IC-12 | Ih | B12H122- |
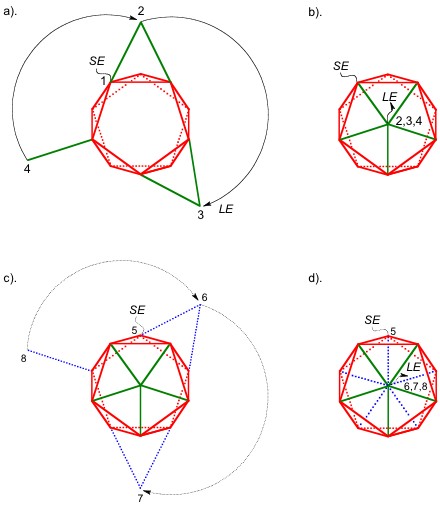
IV Conclusion.
Polifacil models have received good acceptance as a
teaching and learning material of the spatial geometry, from basic
school to undergraduate and graduate levels. For example, during
several "National Weeks of Science and Technology" promoted
in our country by the Council of Science and Technology of Mexico
(CONACyT) and in our city by Council of Science and Technology
of Puebla (CONCyTEP), many teachers of mathematics invited us
to make workshops for teaching the Polifacil system to
their children (Figure 11).
On the other hand, we have developed static (e. g. models of carbon's hybrids: Fuentes-López, 2005) and dynamic models (e. g. model for illustrate the fluxional behavior in 5-coordinated atoms; Pérez-Benitez, 1992) based on the Polifacil system which will be presented later. In all of these cases the simplicity and versatility of this system, besides the low cost of the starting materials make to the Polifacil models a very attractive and useful way of learning and teaching the spatial geometry.
|
|
|
|
|
|
V Notes and references.
a) We coined the word "Polifacil"
for naming in Spanish to this construction system of polyhedra;
it is composed by two words: Poli and facil coming
respectively from poliedro (polyhedron) and facil
(easy). The orthographic accent in the letter "a"
was suppressed for the html presentation.
b) Raffia is a plastic ribbon based on rayon or polypropylene. It can be bought in any haberdashery.
c) In the Figures 2, 3, 5, 7 and 8, the straws are represented by red, blue or green straight lines while raffia is in black curved lines. Moreover, the ends of the straws or the vertices are numbered for a better understanding of the procedure.
1) Arroyo-Carmona, R. E.; Fuentes-López, H.; Méndez-Rojas, M. Á.; Pérez-Benitez, A. "La geometría: ¡Un pie que cojea en la enseñanza de la estereoquimica". Educ. Quim. 16 (Núm. Extraord.), 2005, pp. 184-190.
2) Borglund, E. "Avec de la paille". Ed. Sélection J. Jacobs. Paris, 1972. pp. 36-37.
3) Fuentes-López, H. "La construcción de modelos tridimensionales como estrategia didáctica para la enseñanza-aprendizaje de las hibridaciones del carbono a nivel licenciatura". Thesis of master of education in sciences. Faculty of Chemical Sciences. Benemérita Universidad Autónoma de Puebla. January, 2005.
4) Hartshorn, R.M.; Hey-Hawkins, E.; Kalio, R.; Leigh, G. "Representation of configuration in coordination polyhedra and the extension of current methodology to coordination numbers greater than six". Pure Appl. Chem. 79 (10), 2007, pp. 1779 -1799.
5) Pérez-Benítez, A.; González-Vergara, E. "Un tetraedro (o un tetraedro alargado) a partir de un popote y un cordel". Educ. Quím. 1991, 2, p.p. 198-200.
6) Pérez-Benítez, A.; González-Vergara, E. "Taller de construcción de poliedros moleculares". III Congreso Iberoamericano, X nacional de química inorgánica y II simposio de química del silicio. Zacatecas, Zac. April, 1991.
7) Pérez-Benítez, A.; Arroyo-Carmona, R. E. "¿Sabes qué es un hexaedro? La respuesta y un modelo plegable elaborado con materiales de desecho". Saberes Compartidos. 2008, 2, pp. 50-54.
8) Pérez-Benítez, A.; González M. R.; González-Vergara, E. "Un modelo dinámico sencillo para ilustrar la pseudorrotación de Berry". Rev. Soc. Quím. Méx. 36, 1992, p. 96. Abstract C/31.