Chemical Education Journal (CEJ), Vol. 16/Registration No.
16-104/Received July 1, 2014.
URL =http://chem.sci.utsunomiya-u.ac.jp/cejrnlE.html
Abstract
Classical thermodynamics provides a straightforward interpretation
for 'entropy production' in terms of 'lost-work'. Despite its
potential utility in the undergraduate classroom to bring a concrete
perspective to the causes and effects of irreversible processes,
rarely is this connection found in elementary physical chemistry
or thermodynamics textbooks, nor its use suggested or exemplified
in the chemical education periodical literature. It is with the
intention of providing the interested instructor with classroom
material for an initial presentation of this approach, that this
paper has been written. The examples discussed, relevant to introductory
physical chemistry or thermodynamic courses, include an ideal
gas expansion, the mixing of ideal gases, the flow of heat between
two heat reservoirs, and an adiabatic and irreversible process.
Keywords: Thermodynamics, irreversible processes, entropy production, lost work
2 Entropy production as a gauge of lost work in irreversible processes
3 The Free-Expansion of an Ideal Gas
4 The Mixing of Two Ideal Gases
5 An Irreversible Heat Transfer
6 An Irreversible and Adiabatic Expansion
The total entropy change measures the lost work when a process falls short of (the) idealized condition. Entropy reminds us that something we value has been lost--work. [Kyle, 1999]
The entropy change of the system plus surroundings may be viewed as a quantitative measure, or index, of the degradation of energy as work to energy as heat, as a consequence of irreversible elements in the process under study. [Weber and Meissner, 1957]
The fact that the connection between lost-work and entropy production finds precise thermodynamic definition [Smith and Van Ness, 1965a] alongside the fact that this connection can be properly exemplified via the efficiency of chemical processes [Tolman and Fine, 1948; Kjelstrup and Bedeaux, 2001] might suggest the extended use of this venue to bring meaning to the usually elusive concepts of entropy and entropy change. Judging, however, from the contents of introductory thermodynamics and physical chemistry textbooks it is safe to say that this 'lost-work' approach is sidetracked by that incorrectly identifying entropy production with an increase in chaos, disorder, or randomness [McGlashan 1966, Lambert 2006]. The problem with this last didactic approach residing in the fact that, in the words of Brostow "...one tries to connect an indeed quantitative and exact notion, entropy, with something called disorder, which is loose and subjective and for which no definition exists..." [Brostow, 1972]
The discussion herein presented intends to provide the thermodynamics instructor with classroom material to illustrate the connection between entropy production and lost-work. Hopefully this material will contribute to a better understanding of this cardinal thermodynamic concept.
...The second law of thermodynamics states that there exists in nature for each system of bodies a quantity, which by all changes of the system either remains constant (in reversible processes) or increases in value (in irreversible processes). This quantity is called, following Clausius, the entropy... [Planck1990a]
Actual processes are irreversible, and every irreversibility results in lost work. [Smith and Van Ness 1965b]
The fact that according to the previous quotes every irreversible process is accompanied by the production of entropy as well as the production of lost-work strongly suggests the existence of a connection between these two magnitudes. That this is indeed the case is the matter of the following argument which compares the effects of the reversible (rev) and irreversible (irr) isothermal (T) paths of a thermodynamic system (s) from a given initial (i) to a given final condition (f), as depicted in Figure 1. In these processes the surroundings are constituted by a heat bath or heat reservoir (HR) of the same temperature (T) as that of system, and of a mechanical reservoir (MR) to store/supply the work produced/demanded by the process. Combined, system and surroundings, define the universe (u) of the process. The fact that the initial and final conditions are common to both of these paths allows us to designate one as the reversible counterpart of the irreversible other, and vice versa.
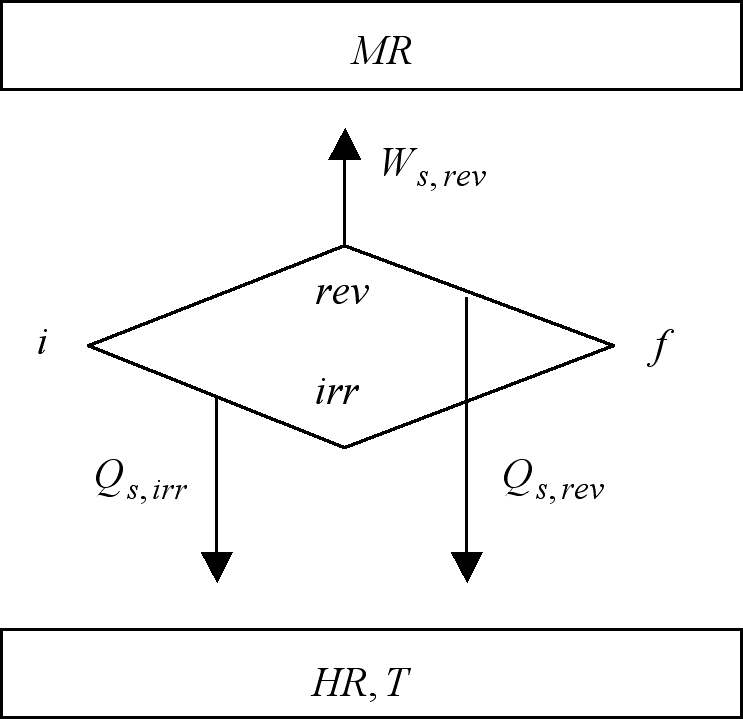
Figure 1. The reversible (upper locus) and irreversible (lower locus) evolutions of a thermodynamic system between the same initial (i) and final states (f) are here depicted. The work output of the reversible path is the maximum possible at the particular conditions of the process. The irreversible path to which the figure makes reference outputs no work at all i.e. Ws,irr = 0
Let us start by defining lost-work as the difference between the system's reversible and irreversible work outputs, i.e.
|
|
(1) |
The first law allowed replacement of these work outputs by their respectively associated heat and energy changes, i.e.
and
in combination with the fact that on reason of the initial and final states being common to both of these paths it is true that
|
|
(2) |
The realization that the only two bodies capable of heat exchange are the system and the heat reservoir (HR) allows us to understand that heat lost by one is heat absorbed by the other, or vice versa, i.e.
This expression allows us to write equation (2) as follows
|
|
(3) |
In equation (3) the terms QHR,rev and QHR,irr refer, respectively, to the heat exchanged by the heat reservoir along the system's reversible and irreversible paths. This equation sheds light on the fact that the work lost in the irreversible process appears as that extra amount of heat rejected to the heat reservoir in excess of that rejected in the reversible path.
The fact that the entropy change for a heat reservoir is determined by the quotient of the actual amount of heat by it exchanged divided by its temperature [Denbigh 1968] allows us to transform equation (3) as follows
|
|
(4) |
The following equations will now be written for the entropy changes of the universes of the two paths being considered
|
|
(5) |
|
|
(6) |
The consideration previously made in regard to the equality of the internal energy changes for the two paths connecting the same initial and final conditions, can now be made for the entropy state function i.e.,
|
|
(7) |
This result allows expressing the subtraction of equation (5) from equation (6) in the following way
|
|
(8) |
The previous result, on reason of equation (4), can be written as
|
|
(9) |
The fact that the total entropy change for any reversible process is zero (ΔSu,rev = 0), in combination with the following definition
|
|
(10) |
allows us to finally write the following equation for the entropy change of the irreversible universe
|
|
(11) |
A most important notion subsumed by equation (9) can now be unveiled via the realization that in it the equal sign is a statement of the fact that the effects which measured by ΔSu,irr are left in its universe by the irreversible path, are identical to the effects which measured by ΔSu,rev + (Wlost / T) are left in its own universe by the concatenation of the reversible counterpart, in which an amount of work Wrev is produced, with that step in which either a part or the whole of this work is irreversibly lost as heat in the heat reservoir. The fact that the total entropy change for the reversible counterpart is zero illuminates the fact expressed by equations (10) and (11) that the production of entropy in irreversible processes finds origin and quantification in the work lost in those processes. The previous considerations have been represented in Figure 2.
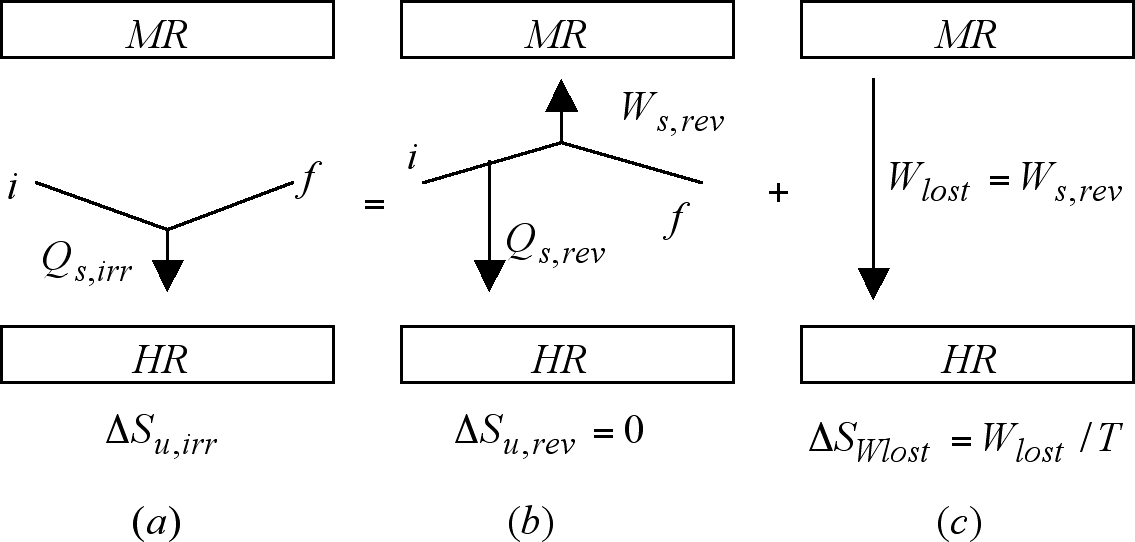
Figure 2. The notion subsumed by equation (9) that the effects of an irreversible process are identical to those of its reversible counterpart plus a work degrading step has been here represented. An excellent classroom didactical recourse consists in tying the progression of the work-degrading step to the rotation of path (b) along the i-f axis. Once the work-degrading step concludes, path (b) ends its 90o rotation adopting or collapsing into the irreversible path.
The argument leading to equation (9) can be easily extended to include that case in which it is necessary to incorporate an additional heat reservoir of temperature T*, colder than that with the same temperature of the system. We can assume here that the heat made available by the irreversible evolution of the system, or by the work degrading step in its equivalent concatenation, is first absorbed by the original reservoir, with an associated entropy change of Wlost / T; only to be transferred to the colder reservoir producing here an entropy change of (-Wlost / T) + (Wlost / T*). The combination of these two entropy changes leaves us with Wlost / T*. At the end, the original reservoir remains unchanged, being the lowest temperature one the one determining the magnitude of the irreversible entropy change. Earlier and alternative discussions of these issues can be found in the literature [Balzhiser et. al. 1974; DiLiberto 2007]
The objective of the examples presented below is to show that irreversible entropy production finds origin and quantification in the degradation of work into heat at the temperature of some heat reservoir. In the first three examples the selected irreversible processes evolve without the output of work, in other words, for all of them
Under this condition, in which equation (1) reduces to
all the work produced by the reversible counterpart is to be irreversibly transferred as heat to the heat reservoir. The fourth example, dealing with an adiabatic and irreversible expansion, differs from the previous three in three regards: that the calculations will be performed numerically; that here the irreversible process will be capable of outputting a certain amount of work,
and finally, that in addition to that step in which an amount of work of magnitude
is to be degraded, the concatenation will require of two reversible processes to produce the required transit from initial to final conditions.
The need to discriminate via sub-indexes between the energy exchanges of system and surroundings will be no longer necessary in the discussions that follow. All the energy magnitudes there will be referred to the system.
The significance of the second law of thermodynamics depends on the fact that it supplies a necessary and far reaching criterion as to whether a definite process which occurs in nature is reversible or irreversible...A process which can in no way be completely reversed is termed irreversible, all other processes reversible. That a process may be irreversible, it is not sufficient that it cannot be directly reversed....The full requirement is, that it be impossible, even with the assistance of all agents in nature, to restore everywhere the exact initial state when the process has once taken place. [Planck 1990b]
Figure 3 (a) depicts the occurrence of an ideal gas free-expansion. Here, one mole of the gas transits, in an irreversible fashion, between initial and final states defined respectively as (Pi,Vi,T) and (Pf,Vf,T).
On reason of the expansion taking place against a vacuum the ideal gas performs no external work, i.e.
Furthermore, the non-existence of intermolecular forces between its constitutive particles means that no energy needs to be spent in separating them as the expansion proceeds, and if so, no demand of energy, either in the form of heat from its surroundings,
nor as internal energy from itself,
is made for the performance of this task. The constancy of the ideal gas internal energy translates, in turn, in a constant temperature (T) evolution. The total entropy change for one mole of gas undergoing this process is known to be [Klotz and Rosenberg 1986a]
|
|
(12) |
Let us now focus our attention on process 3(b) i.e., on the first step of the concatenation of processes represented in the right-hand side of Figure 3. Along this process, one mole of the same ideal gas expands in an isothermal (T) and reversible fashion between the same initial and final states as those defining the irreversible expansion of Figure 3 (a), and in doing so it manages to transform into work (Wrev) an equivalent amount of heat (Qrev) absorbed from the heat reservoir (HR) also of temperature T. The total amount of work performed (transferred) by the system on (to) the mechanical reservoir (MR), has, for the initial and final conditions given, the following magnitude [Maron and Prutton, 1965a]
|
|
(13) |
As indicated in Figure 3 (c), at the conclusion of the isothermal and reversible expansion the work by it produced (Wrev) is retrieved from the mechanical reservoir to be degraded, say via a frictional mechanism, into an equivalent amount of heat at the temperature of the heat reservoir. The fact that in the irreversible process no work is produced (Wirr = 0) serves to explain, via equation (1), which under this condition reduces to
the need to degrade the whole of the reversible work. The entropy change sustained by the heat reservoir on reason of this irreversible step, determined as indicated by equation (10), has the following value
|
|
(14) |
A simple contrast between equations (12) and (14) serves as confirmation of the fact that the total entropy change for the free-expansion finds quantification in a work-degrading step.
It should be noted that in the free-expansion there is no interaction whatsoever between the expanding gas and the reservoirs, i.e. they experience no change as a consequence of this process. This is the reason why they are not depicted in Figure 3 (a). In the reversible expansion step 3 (b), however, both reservoirs are affected. While the heat reservoir releases an amount of heat Qrev, the mechanical reservoir receives, on its part, an equivalent amount of work Wrev. Both of these changes are, it should be noticed, reversed in the work-degrading step 3 (c). While the mechanical reservoir recuperates its initial condition once Wrev is retrieved from it; the heat reservoir does it upon absorption of the heat resulting from the work degrading step. At the end we find that the final condition of the universe in the free-expansion and that of the concatenation's universe is one and the same, as both have produced an irreversible universe containing as sole change an expanded gas with conditions (Pf,Vf,T).
It is important to note here that previous to the work-degrading step, the right hand side universe is indeed reversible. This is so because the work available in the mechanical reservoir (Wrev) is precisely that required to restore the initial condition of the three bodies here involved. To understand this let us start retrieving Wrev from the mechanical reservoir and use it to reversibly compress the gas to its initial condition. In doing so, the spent work will find its way to the heat reservoir. At the end of these events we will find both reservoirs as well as the gas in their respective initial conditions, without changes being left elsewhere. Once the work degrading step is over the situation is, however, radically different. Here the compression of the gas cannot be carried on unless a change is left in that body called to supply the work we no longer have. The loss of Wrev brought about by the work-degrading step is the reason behind the transition of the right hand universe from reversible to irreversible.
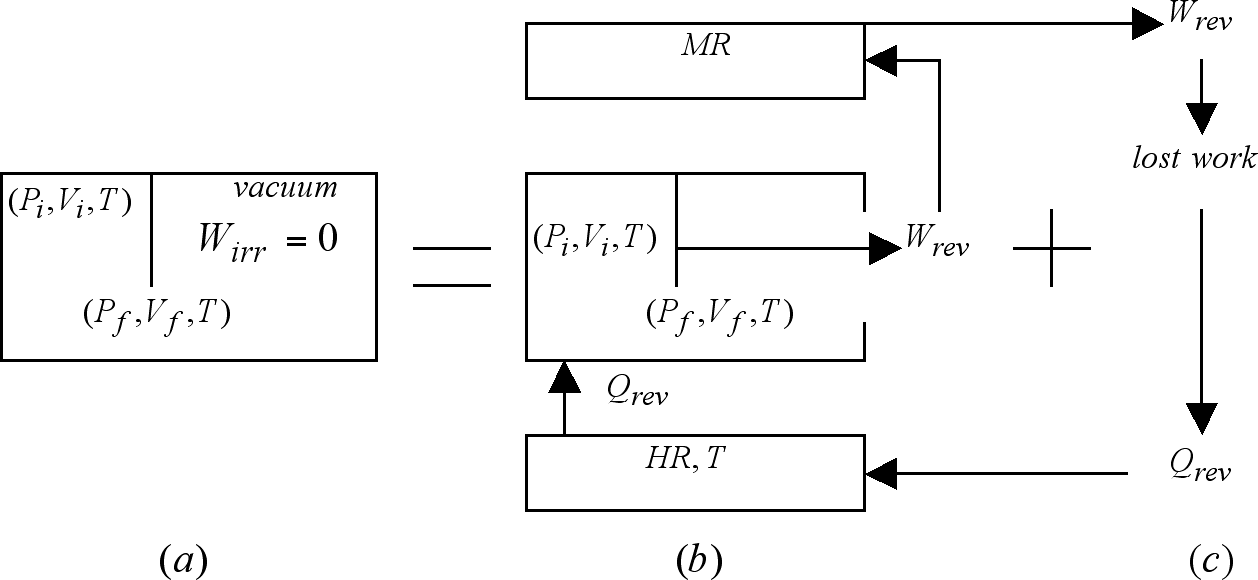
Figure 3. The effects of the irreversible, work-less, ideal gas free-expansion shown in (a) transiting between initial and final states (Pi,Vi,T) and (Pf,Vf,T), are reproduced by those of the concatenation of the reversible and isothermal expansion transiting between the same initial and final conditions shown in (b), in which an amount of work Wrev is produced, with that process shown in (c) in which this work Wrev is degraded into heat at the temperature of the heat reservoir.
It is true that process 3 (a) outputs no work. The lost-work to it associated --of the same magnitude than that quantifying its entropy change, is the one it could have produced, but did not. In its transit from its initial to its final condition this process wasted, dissipated its work producing potential. The fact that its entropy change is identical to that of process 3 (c) is an indication of the fact that for thermodynamics the wasted dissipation of work producing potential taking place in 3 (a) is entropically indistinguishable from the irreversible degradation of actual work into heat taking place in its 3 (c).
In Figure 4 (a) we see nA moles of ideal gas A occupying a volume VA at temperature T and pressure P; and nB moles of ideal gas B confined in a volume VB at the same temperature and pressure. The contiguous chambers containing the gases are separated by a movable partition. When this partition is suddenly removed, the gases will irreversibly mix without the production of work or the exchange of heat. That this is so can be understood by realizing that in ideal gas mixtures "...every gas is a vacuum to every other gas..." [Gibbs, 1906]. From this perspective volume VB is nothing but empty space for gas A, and vice versa. Under these conditions the mixing process becomes nothing more than the simultaneous free-expansions of gases A and B from their respective initial volumes to a common, shared volume equal to VA + VB. As discussed in the previous example, these isothermal free-expansions evolve without any interaction with its surroundings. The entropy change for each of these expansions can then be written in accord to that expressed by equation (12). When this is done, and the results combined to produce the total or universe entropy change for this irreversible mixing we get
|
|
(15) |
Let us now center our attention on the reversible mixing step constituting the first step of the concatenation depicted in the right hand side of Figure 4. In this process, represented there as 4 (b), we find the same amount of gases at the same conditions as those of Figure 4 (a). The difference being that they are now separately confined in the cylinder/pistons device there shown. Here the movable pistons have been appropriately fitted with semi-permeable membranes.
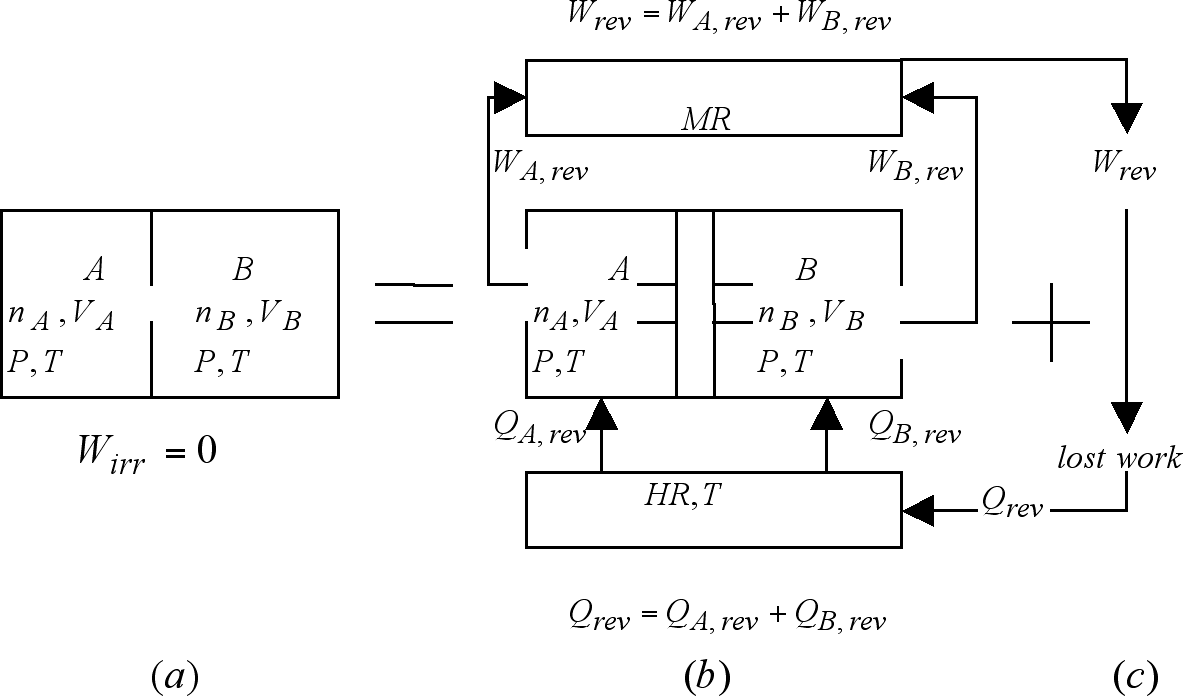
Figure 4. The irreversible ideal-gas mixing process
shown in (a) is equivalent to the concatenation of the reversible
mixing process shown in (b), with the work degrading process shown
in (c). The common final condition for mixing processes (a) and
(b) plus (c) is constituted by the mixture of the indicated number
of moles of species A and B occupying a volume equal
to the combined original volumes, at T and P.
This device, which has been coupled to a mechanical reservoir,
is also in thermal contact with a heat reservoir of temperature
T. The left hand side piston incorporates a membrane permeable
only to gas A, and the right one a membrane permeable only
to gas B. Being this so, the gases mix upon reaching the
space between the pistons. Even if these gases exert no force
on their respective pistons, they exert their respective pressures
on the opposite ones. Achieving a reversible mixing with this
device calls for the application to the left hand side piston
of an external pressure opposite and infinitesimally smaller than
that exerted on it by B, as well as of the similar application
in the right hand side piston of a pressure equally smaller than
that exerted on it by A [Klotz
and Rosenberg 1986b]. The continued diffusion of the gases
through these membranes marks the transit of gases A and
B from their respective smaller initial volumes VA and VB to
the larger and common volume VA
+ VB. Thus perceived the mixing
process turns out to be nothing more than two simultaneous expansions,
two isothermal and reversible expansions if note is taken of the
constraints upon which they proceed. In them the heat bath assures
the constancy of temperature of the gases by providing the heat
demanded by the expansion work
produced by the opposed and outward motion of the pistons which, according to equation (13), has the following magnitude
|
|
(16) |
As indicated in Figure 4 (c), the retrieval of this work from the mechanical reservoir followed by its degradation into an equivalent amount of heat at the temperature of the heat reservoir will produce the return of both reservoirs to their respective initial conditions. The mechanical reservoir will be stripped of the work originally deposited in it, and the heat reservoir will recuperate the heat it originally released. The indicated concatenation of 4 (b) and 4 (c) produces this way an irreversible universe indistinguishable from that depicted in the left hand side universe: An ideal gas mixture of the indicated amounts of A and B at temperature T in a volume VA + VB. The un-mixing of these gases can be produced by reversing the motion of the pistons i.e. by reversible compressing each of the two gases to their initial conditions. This process, however, demands the expenditure of an amount of work that we no longer have. If done, it will be at the price of leaving a change in that body called to supply this work. Once the work is lost, the universe becomes irreversible. The fact that process 4 (a) outputs no work (Wirr = 0) serves to explain, via equation (1), the need to degrade the whole of the work outputted by its reversible counterpart, as here, according to equation (1):
The entropy change for process 4 (c), calculated via the quotient of equation (16) divided by T , has the following magnitude
|
|
(17) |
The comparison of this result with that given by equation (15) allows us to see, again, the entropy change of an irreversible process finding quantification in a work degrading process.
Figure 5 (a) depicts the irreversible, work-less transfer of an amount of heat Qh from a hot reservoir of temperature Th to a cold reservoir of temperature Tc. This process, which takes place with the sole involvement of the heat reservoirs, is known to have associated the following entropy change [Klotz and Rosenberg 1986c]
|
|
(18) |
In what follows it will be shown that the effects left on their universe by the combined action of processes 5 (b) and 5 (c) are identical to those left in its own universe by the said irreversible transfer of heat. In 5 (b) we have depicted the two effects brought forward by one cycle in the operation of a reversible Carnot engine; these being the transformation into work (Wrev) of the portion Q of an amount of heat Qh absorbed from the hot reservoir of temperature Th, and the transfer of the remaining portion Qc to the cold reservoir of temperature Tc. Here
with
In process 5 (c), the second leg of the concatenation, we see the work produced by the reversible engine (Wrev) being retrieved from the mechanical reservoir to which it was originally transferred, only to be degraded, via a frictional process, into heat at the temperature of the cold reservoir.
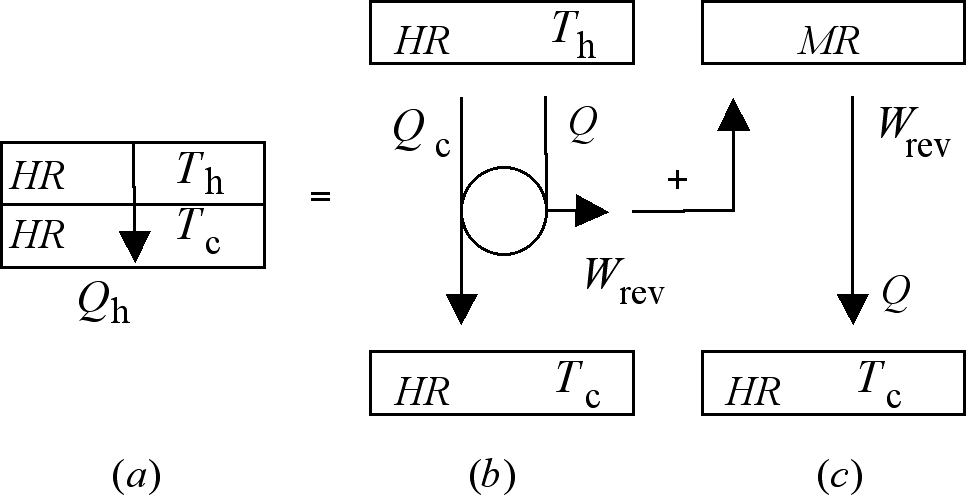
Figure 5. The irreversible transfer of the amount of
heat Qh shown in (a) is here reproduced
by the concatenation of a first step represented by one cycle
in the operation of the reversible heat engine shown in (b), in
which an amount of work Wrev is
produced, with a second step represented by that process in which
this work is degraded into heat at the temperature of the cold
reservoir.
That the concatenation of processes 5 (b) and 5 (c) reproduce
the effects of the irreversible heat transfer depicted in Figure 5 (a) can be understood by taking
notice of the following facts. First, that on completion of one
cycle in its operation, the heat engine--represented by the central
circle in 5 (b)--returns to its original condition, so no change
remains in it. Second, that on release of the work in it deposited,
the mechanical reservoir also returns to its initial state. If
so, all the changes left by the concatenation can be traced to
the heat reservoirs. When these changes are identified they are
found to be identical to those sustained by the heat reservoirs
of process 5 (a); these being the release of Qh
by the hot reservoir in 5 (b); and the absorption, in two steps,
of the same amount of heat by the cold reservoir: Qc
along the cyclic evolution of the engine in 5 (b), and Q
from the work degrading process in 5 (c). The common, irreversible
condition these universes find themselves in at the conclusion
of their respective processes stems from the fact that in none
of them there is any work available with which to bring them back
to their respective original conditions. Any restoration, be it
in 5 (a) or in the concatenation, would be at the price of permanent
changes being left in the body or bodies called to provide the
work demanded by such a task. The identity of effects existing
between these two processes implies the same entropy change for
both of them. To prove that this is so starts by bringing here
the accepted total entropy change for one cycle in the operation
of the reversible engine shown in 5 (b) [Pitzer
and Brewer, 1961]
|
|
(19) |
The first term of the right hand side of the previous equation is formed by the entropy changes sustained by the hot reservoir of temperature Th in releasing an amount of heat Qh, and that experienced by the cold reservoir of temperature Tc upon absorption of the amount of heat Qc to it released by the engine. The second term has been obtained via substitution of
followed by the grouping of like terms there shown. As originally done by Clausius [Clausius, 1879], this grouping allows identifying the term between the brackets as the entropy change for the reversible transfer of Qc from the hot to the cold reservoir; and the last term with the entropy change associated to the transformation of Q into Wrev.
If Wrev is now retrieved from the mechanical reservoir and irreversibly degraded into heat at the temperature of the cold reservoir, entropy will be produced in the amount indicated by equation (10), i.e.
|
|
(20) |
The total entropy change for the concatenation can be now quantified by the combination of equations (19) and (20) as follows
|
|
(21) |
When equations (18) and (21) are compared at the light of equation (9) we can see, again, the entropy change of an irreversible process being quantified by the entropy change associated to a work-degrading step.
Let us note here, en passant, that in the total entropy change for the reversible heat engine, as written in the rightmost term of equation (19), the entropy change attributed to the reversible transfer of Qc is formally identical with the one ascribed to the irreversible transfer as given in equation (18). This fact, nothing short of peculiar, can be taken to imply the reversible engine's universe subsuming an irreversible heat transfer or, equivalently, a reversible heat transfer being entropically indistinguishable from an irreversible one.
Further discussions on this issue can be found in the literature [Íñiguez 1999].
The initial state for this example will be one mole of ideal gas Argon confined in a thermally insulated container of the cylinder/piston kind at the following conditions:
Ari (2 bar, 450 K, 18.71 dm3).
For this gas it is known that
Cp = 20.92 J K-1mol -1, Cv = 12.59 J K-1mol -1
and g = Cp / Cv = 1.66 [Maron and Prutton, 1965b].
The values used for the gas constant R were 0.08314 bar dm3K-1mol -1 and 8.314 J K-1mol -1.
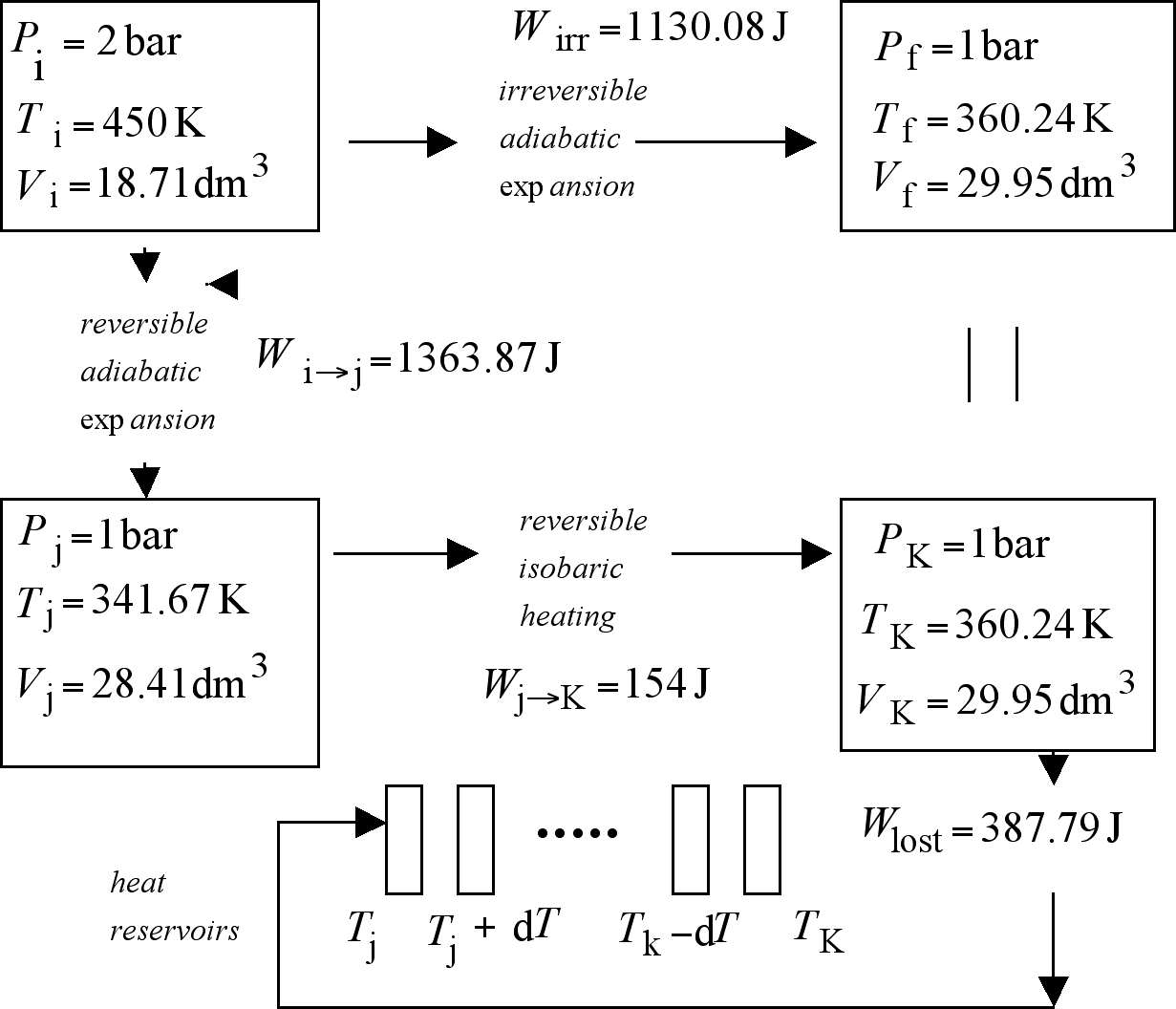
Figure 6. The reproduction of the effects produced by the irreversible and adiabatic ideal gas expansion shown above, demands the concatenation of two reversible processes--an adiabatic and reversible expansion followed by a reversible isobaric heating--with a work degrading process. The entropy change for the irreversible expansion is identical to that associated to the degradation of the amount of work Wrev - Wirr into heat at the temperature of the coldest available heat reservoir.
The gas is now subject to an irreversible adiabatic expansion against a constant external pressure Pext = 1 bar. In order to determine the rest of the conditions of the gas at the end of this expansion use will be made of the fact that here q = 0, and consequently
For our system, this equation can be written as
and after replacement of the volumes for their corresponding RT / P re-expressions, followed by rearrangements and simplifications, as
[Dickerson, 1969]. Upon substitution of the known data for the initial state, the heat capacities, as well as Pf = 1 bar, we get for the final temperature a value of Tf = 360.24 K. Use of the perfect gas law with the appropriate data gives us the final volume, Vf = 29.95 dm3. The irreversible work performed by the gas in this expansion can now be calculated as
Using the appropriate data we get Wirr = 1130.08 J.
The final state of this irreversible adiabatic expansion can now be specified as
Arf [(1 bar, 360.24 K, 29.95 dm3), Wirr = 1130.08 J].
The total entropy change for the universe of this process is, as should be obvious, also that of the expanding gas. It can be evaluated via the integrated expression of the first and second laws combined,
[Moore, 1972]. Upon substitution of the proper values it produces the following result
|
|
(22) |
In what follows we will transit between the same initial and final states, but now this will be done through a path constituted by the concatenation of three processes: a reversible and adiabatic expansion, a reversible and isobaric heating, and a work degrading step.
The first of these processes will start at Ari (2 bar, 450 K, 18.71 dm3) and end up at condition 'j ' characterized by a value for the pressure identical with that ruling at Arf, i.e. Pj = 1 bar. With this variable specified, we can proceed to determine the values of the other variables at this state. This will be done with the equation describing the path of this process,
Substitution here of the available data leads to Vj = 28.41 dm3. Further substitution of Pj and Vj in the ideal gas law produces the following value for the temperature at this condition, Tj = 341.67 K; therefore Arj (1 bar, 341.67 K, 28.41 dm3). The reversible work produced by this process, evaluated with
At the conclusion of this process, the gas is subject to a reversible and isobaric heating. This reversible process, concluding at condition k, takes place against a constant external pressure of 1 bar. The heating increases the temperature of the gas until it is identical with that characterizing Arf, i.e. Tk = 360.24 K. At this point Pk = 1 bar and, according to the ideal gas law, Vk = 29.95 dm3. The reversibility condition of this process is satisfied by making use of an infinite number of heat reservoirs bound by those with temperatures 341.67, 341.67 + dT and 360.24 - dT, 360.24 [Nash 1970]. The reversible work produced by this process, evaluated as Pk(Vk - Vj), amounts to Wrev,j→k = 154 J. The concatenation of these two reversible processes, with a combined total entropy of zero, has managed to take the gas from Ari (2 bar, 450 K, 18.71 dm3) to condition Ark (1 bar, 360.24 K, 29.95 dm3), identical in regard to the condition of the gas, with Arf. Let us now recognize that even if the gas at state 'k ' is in the same condition as that in state 'f ' , the same cannot be said about the universe, and this is so because while in the former the mechanical reservoir is safekeeping an amount of work
in the latter the available work amounts to Wirr = 1130.08 J.
For the universes at 'k ' and 'f ' to coincide we have to make sure the same amount of work remains available in both of them. For this to happen, we will have to reduce to 1130.08 J that available in 'k ', and for this to happen we have to degrade, to lose as heat into the coldest heat reservoir available in the universe an amount of work equal to
Wlost = 1517.87 J - 1130.08 J = 387.79 J.
When carried on, this irreversible step will produces, as shown in equation (23), an entropy increase identical--within the precision (~2%) of the (TI-86) calculations--to the previously quoted ΔSu,irr = 1.11 J K-1 corresponding to the direct path.
|
|
(23) |
The previous result allows us to see, one more time, the re-expression of lost-work as an entropy increase.
It should be noted here that the decision to fix at 1 bar the
pressure at the end point of the reversible adiabatic expansion,
even if arbitrary, is however convenient as it brings us closer
to the desired end state k (or f ). Other values
for the pressure or a different variable could have been chosen
to fix this expansion. With each choice, however, comes the added
task of finding the next reversible step or steps that could take
the system to the desired end state. [Klotz
and Rosenberg 1986d].
The analysis of reversible and irreversible chemical reactions
at the light of equation (9) has been
the subject of a previous published work by this author [Íñiguez
2014]. Its classroom presentation as part of the set of cases
above discussed is strongly recommended.
It is this author's experience that more often than not a positive response from students of thermodynamics follows classroom presentations in which the concepts considered are discussed from different perspectives, an approach sure to bring reinforcement of concepts already learned, and clarity to those being seen for the first time. This paper was written with the intention of collaborating with those in charge of the not easy job of making classroom discussions of chemical thermodynamics lively as well as relevant.