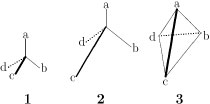
Figure 1 Three models for a tetrahedral molecule with the ligand pattern Cabcd [6].
Chemical Education Journal (CEJ), Vol. 8, No. 2 (Serial No. 15). The date of issue: April 11, 2005./ Registration No. 8-8/ Received November 22, 2004.
URL =
http://www.juen.ac.jp/scien/cssj/cejrnlE.html
E-mail: fujitas@chem.kit.ac.jp
Abstract:
The desymmetrization of a regular tetrahedral molecule
is discussed by emphasizing the importance of orbits,
which appear concurrently in the molecule as
equivalence classes of objects
such as atoms (vertices), bonds,
edges (hypothetical lines containing two atoms),
faces (hypothetical planes containing three or more atoms),
bond angles, and any other segments.
Each orbit is ascribed to a sphericity index,
which is determined by the sphericity and the size of the orbit.
Concurrent desymmetrizations of such orbits
are characterized by unit subduced cycle indices
with chirality fittingness (USCI-CF), which are
defined as the product of such sphericity indices.
Thereby, the validity of models based on the
regular tetrahedron is proved systematically.
In introductory courses of organic stereochemistry, regular tetrahedron models (e.g., 1) have been used to teach chirality/achirality, Cahn-Ingold-Prelog sequence rules, and related stereochemical items [1, 2, 3]. Irregular tetrahedrons have been also adopted to characterize models having different bond lengths and bond angles [4, 5]. Recently, Lloyd-Williams and Giralt [6] discussed the desymmetrization of tetrahedral molecules by considering regular tetrahedron models (model 1), models with tetrahedral geometry around the central atom, but with varying C-substituent bond lengths (model 2), and irregular tetrahedral models (model 3), as shown in Fig. 1. Their conclusion is that stereochemical issues in the molecules Cabcd, where chirality may be analyzed as being the result of the presence of a stereogenic center, can be fully explained using a model based on the regular tetrahedron 1, even though this model does not take into account different substituents causing the molecule to have different bond lengths (e.g., in 2) and bond angles (e.g., in 3) [the emphasis and the comments in parentheses are added by the present author].
Although the discussion by Lloyd-Williams and Giralt [6] aimed at the education of undergraduate level, the conclusion implies an essential viewpoint on the equivalency of such models, where the viewpoint is also useful to graduate students and researchers. It should be noted, however, that their discussion was restricted within Td, C3v, C2v, Cs, and C1, whereas Fujita [7] further described T, S4, C3, and C2 by taking chiral substituents into consideration. Moreover, both of the discussions did not deal with the reason of why the point groups D2d and D2 among the subgroups of Td does not appear. Hence, a more elaborate examination is desirable to deal also with such cases as containing chiral and achiral substituents.
In the present paper, the essential viewpoint will be further discussed by virtue of a new method based on orbits (equivalence classes) and sphericity indices, which has been recently reported by Fujita [8, 9] . Concurrent desymmetrizations of orbits appearing in a molecule will be emphasized as a key concept to clarify the equivalency of such models 1, 2, and 3. Thereby, graduate students and researchers along with undergraduate students will be able to gain a deeper insight into stereochemistry.

Figure 1 Three models for a tetrahedral molecule
with the ligand pattern Cabcd [6].
To manipulate symmetrical properties of molecules, an orbit (an equivalence class) is defined as a set of equivalent objects contained in a molecule, where the equivalency of the objects is determined by operations of the corresponding point group. Such objects can be selected variously according to problems to be answered, e.g., atoms (vertices), bonds, edges (hypothetical lines containing two atoms), faces (hypothetical planes containing three or more atoms), bond angles, and any other segments.
Let us consider the desymmetization of a methane molecule (4) of Td-symmetry into a chlorofluoromethane molecule (5) of Cs-symmetry. It is an easy task to find equivalent atoms (or bonds) and to regard them as constructing an orbit. The equivalency of objects of other types can be also found by a slightly careful inspection.

Figure 2 Desymmetrization of methane into chlorofluoromethane.
Table 1 Orbits and sphericity indices in a methane molecule
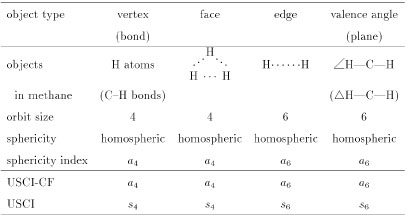
In the methane molecule (4), there appear various types of objects, which are characterized by using Fujita's method [7], as shown in Table 1. First, the four hydrogens in the methane molecule are equivalent so as to construct a four-membered orbit. This orbit is determined to be homospheric, because anyone of the hydrogen atoms is fixed by a rotoreflection (e.g., a mirror reflection with respect to a mirror plane containing H--C--H) [7]. Hence, the orbit is characterized by a sphericity index a4, where the letter a indicates the homosphericity and the subscript 4 represents the size of the orbit [9].
In place of the four hydrogen atoms, the set of four C—H bonds in the methane molecule can be selected as an orbit, which is obviously characterized by the same sphericity index a4. On the same line, the four hypothetical faces, each constructed by each set of three hydrogen atoms (H…H…H), can be recognized to construct an orbit that is characterized by the sphericity index a4.
The six hypothetical edges (H…H) in the methane molecule can be regarded as objects of another kind so that they are so equivalent as to construct a six-membered orbit. This orbit is determined to be homospheric, because anyone of H…H is fixed by a rotoreflection (e.g., a mirror reflection with respect to a mirror plane perpendicular to the edge H…H) [7]. Hence, the orbit is characterized by a sphericity index a6, where the letter a indicates the homosphericity and the subscript 6 represnets the size of the orbit. On the same line, the six H—C—H angles (∠H—C—H) in the methane molecule construct a six-membered orbit, which is ascribed to the sphericity index a6. The six planes (ΔH—C—H) determined by respective H—C—H segments also construct a six-membered orbit, which is ascribed to the sphericity index a6.
Let us consider the chlorofluoromethane molecule (5), which belongs to Cs (Fig. 2). The above-described objects in the methane molecule (Table 1) are influenced by this desymmetrization. Thus, the resulting chlorofluoromethane has orbits of various types as collected in Table 2.
Table 2 Orbits and sphericity indices in a chlorofluoromethane molecule
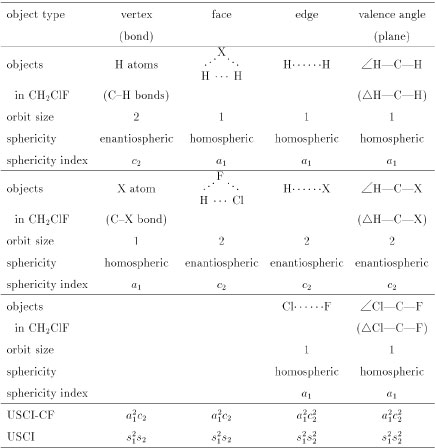
The two hydrogen atoms in the chlorofluoromethane molecule construct a two-membered orbit. According to Fujita's method [7], this orbit is determined to be enantiospheric, because no rotoreflection fixes anyone of the hydrogen atoms. Hence, the orbit is characterized by a sphericity index c2, where the letter c indicates the enantiosphericity and the subscript 2 represnets the size of the orbit. The X atom (chlorine or fluorine) in the chlorofluoromethane molecule constructs a one-membered orbit, which is determined to be homospheric. Hence, the orbit is characterized by a sphericity index a1.
Because the chlorofluoromethane molecule has the one two-membered enantiospheric orbit (H2, c2) and the two one-membered homospheric orbits (Cl or F, each a1), the molecule can be characterized by the product of such sphericity indices as a12c2, which is called unit subduced cycle index with chirality fittingness (USCI-CF). If sphericities are not taken into considered, a unit subduced cycle index without chirality fittingness (USCI) can be used, i.e., s12s2.
On the same line, the objects of other types in the chlorofluoromethane molecule are categorized into orbits, to which sphericity indices are assigned, as shown in Table 2. Thereby, the corresponding USCI-CFs and USCIs are calculated (the bottom of Table 2).
As a result, the desymmetization of the methane molecule (4) into the chlorofluoromethane molecule (5) shown in Fig. 2 is accompanied with concurrent desymmetrizations of the relevant orbits. These desymmetrizations are characterized by comparing the USCI-CFs (or USCIs) collected in Tables 1 and 2, where each USCI-CF (or USCI) in Table 2 is equal to the corresponding sphericity index because of the presence of a single orbit. For example, the desymmetrization a4 → a12c2 for the four vertices and the desymmetrization a6 → a12c22 for the six vertices concur during the process shown in Fig. 2.
For a more general application, the data for methane and chlorofluoromethane are shown below the molecules Ca4 (Td) and Ca2bc (Cs) in Fig. 3, which is a group/subgroup lattice of Td. The other USCI-CFs (and USCIs) for orbits of vertices or edges in Fig. 3 are also obtained in a similar way. It should be noted that one more kind of sphericity appears in chiral molecules belonging T, D, C3, C2, or C1, where the letter b is used to designate the hemisphericity of an orbit [7].
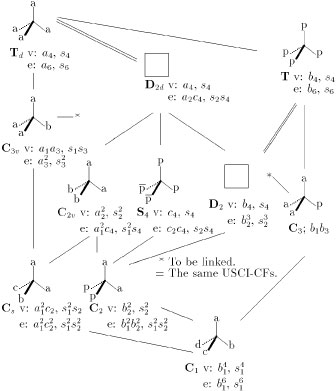
Figure 3 Concurrent desymmetrizations of vertices (v) and edges (e)
monitored by USCI-CFs and USCIs during
the vertex desymmetrizations of tetrahedral molecules.
The letters a, b, c, and d
represent atoms or achiral substituents, while the letters p and \antip{} represent
an enantiomeric pair of chiral substituents.
Even if the regular tetrahedron (1) is used to model the Cabcd molecule, the desymmetrizations of relevant orbits occur concurrently, as designated by the USCI-CF b14 for the vertices and the USCI-CF b16 for the edges of the Cabcd molecule (Fig. 3). The USCI-CF b14 for the vertices is effective to characterize the atoms a, b, c, and d in model 1, to characterize the C—a, C—b, C—c, and C—d bonds in model 2, and to characterize the four faces in model 3. The USCI-CF b16 for the edges is effective to characterize the bond angles of model 3. This means that the consideration of such a model as based on the regular tetrahedron 1 is accompanied with the implicit but inevitable consideration of the same effects as caused by different bond lengths (e.g., in 2) and bond angles (e.g., in 3). Hence, the emphasized phrase in the above-cited conclusion by Lloyd-Williams and Giralt [6] can be omitted according to the present viewpoint.
The discussion by Lloyd-Williams and Giralt [6] was based on the implicit presumption that substituents are regarded as atoms or achiral ligands (groups) and they can be regarded as being structureless. As a result, their discussion omitted T, S4, C3, and C2.
This omission can be explained by using USCIs in place of USCI-CFs. We can find easily that if a given subgroup corresponds to the same USCI as that of a supergroup, a molecule belonging to the given subgroup is absent [10, 11]. As found in the USCI data (v) of Fig. 3, there are the following cases of a supergroup/a subgroup having an equal USCI: Td/T (s4), Td/D2d (s4), Td/D2 (s4), C3v/C3 (s1s3), and Td/S4 (s4). Hence, the molecules of T, S4, C3, and C2 (as well as D2d and D2) were absent in the discussion by Lloyd-Williams and Giralt [6]
On the other hand, Fujita's treatment [7], in which chiral and achiral proligands are permissible as substituents, is explained by using USCI-CFs. We can find that if a given subgroup corresponds to the same USCI-CF as that of a supergroup, a molecule belonging to the given subgroup is absent [10, 11]. The USCI-CF data (v) of Fig. 3 shows the following cases of a supergroup/a subgroup having an equal USCI-CF: Td/D2d (a4) and T/D2 (b4). Because the orbit sizes and the sphericities remain unchanged during the desymmetrizations, the molecules of D2d and D2 are absent even in Fujita's treatment [7]. It should be noted that molecules of T, S4, C3, and C2 appear by taking chiral substituents into consideration. Thus, we have Td/T (a4/b4), C3v/C3 (a1a3/b1b3), and Td/S4 (a4/c4), where the orbit sizes remain unchanged but the sphericities are altered during the desymmetrizations.
The absence of molecules of D2d and D2 means that the USCI-CF data of D2d and D2 shown in Fig. 3 cannot be obtained so long as we stay within the derivation of methane. The following exercises are open to the challenge of readers to solve this difficulty.
Exercise 1: Obtain the data of D2d and D2 by considering a conceptual (i.e., non-experimental) desymmetrization from methane to allene, as shown in Fig. 4, where the central carbon atom of 4 is replaced by an allene unit C=C=C to produce an allene molecule (6).
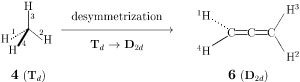
Figure 4 Conceptual desymmetrization of methane into allene.
Exercise 2: Show the appearance of D2d- and D2-molecules by substituting two bidentate substituents (a—a or p—p), as shown in Fig. 5. Explain the results by using the data of edges collected in Fig. 3. See Footnote 7 of [7].
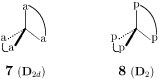
Figure 5 Edge desymmetrization of a tetrahedral model.
Orbits of objects in a molecule, where the objects can be selected to be atoms (vertices), bonds, edges (hypothetical lines containing two atoms), faces (hypothetical planes containing three or more atoms), bond angles, and any other segments, are desymmetrized {\em concurrently} during the desymmetrization of the molecule. Each orbit is characterized by a sphericity index so that each molecule is characterized by a unit subduced cycle index with chirality fittingness (USCI-CF) defined as the product of such sphericity indices. As a result, stereochemical issues in the molecules Cabcd can be fully explained by using a model based on the regular tetrahedron 1, where different substituents causing the molecule to have different bond lengths (e.g., in 2) and bond angles (e.g., in 3) are inevitably taken into consideration in terms of the concurrent desymmetrizations of the relevant orbits.
 Top
Top
