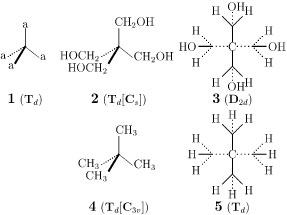
Figure 1 Models of various levels: Tetrahedral promolecule with proligands (left), nonrigid molecule with ligands (center), and molecule fixed at the highest attainable symmetry (right).
Chemical Education Journal (CEJ), Vol. 8, No. 2 (Serial No. 15). The date of issue: April 11, 2005./ Registration No. 8-9/ Received November 26, 2004.
URL =
http://www.juen.ac.jp/scien/cssj/cejrnlE.html
E-mail: fujitas@chem.kit.ac.jp
Abstract:
Molecular symmetries based on a tetrahedral model
are discussed in terms of
subductions of coset representations,
the data of which are obtained manually (non-algebraically)
by examining the local symmetries appearing in the orbits of objects,
e.g., atoms (vertices), bonds,
edges (hypothetical lines containing two atoms),
faces (hypothetical planes containing three or more atoms),
and bond angles.
Because the resulting subduction data
are equivalent to those derived algebraically,
the former are proved to be also effective in the application of
the methods developed previously for the latter
algebraically-obtained subduction data.
This merit has been examined
by tasks for finding molecules matched and mismatched
to local symmetries,
so that the manual derivation of subduction data
is proved to be
a novel way for understanding and teaching the desymmetrization of the tetrahedron in
introductory courses of organic stereochemistry.
In Part I of this series [1], we discussed concurrent desymmetrizations of orbits in a tetrahedral molecule by means of USCI-CFs (unit subduced cycle indices with chirality fittingness) that are derived from sphericity indices [2, 3]. This treatment (called here “the USCI-CF method”) was proved to be useful to judge the equivalency of tetrahedron models of different types (i.e., regular tetrahedron models, models with tetrahedral geometry around the central atom, but with varying C-substituent bond lengths, and irregular tetrahedral models), which have been discussed otherwise by Lloyd-Williams and Giralt [4]. The treatment was also useful to judge the appearance of a tetrahedral molecule of a given point group (a subgroup of Td). These features of the USCI-CF method provided us with a novel way for understanding and teaching the desymmetrization of the tetrahedron in introductory courses of organic stereochemistry.
We have found, however, that we cannot obtain D2d- and D2-molecules among the subsymmetries of Td, so long as we consider the vertex desymmetrization due to the substitution of monovalent substituents (cf. Exercises 1 and 2 of Part I). This is because we have used the USCI-CFs, which only take account of chirality/achirality in terms of sphericities and sphericity indices. In other words, a substituent has been regarded as a structureless object having chirality/achrality only, which has been called proligand [5]. Then a promolecule has been defined as an object in which a given skeleton is substituted by a set of such proligands. Thus, the conclusion of Part I has presumed the concepts of proligand and promolecule, although this presumption has not been described explicitly in Part I.
When a proligand is replaced by a ligand having structure in order to convert a promolecule into a molecule, the resulting molecule may be unexpectedly desymmetrized [5]. For example, suppose that each of proligand ‘a’ in the Ca4-promolecule (1) is replaced by a hydroxymethyl ligand, which belongs to Cs-symmetry in isolation (Fig. 1). The symmetry of the resulting molecule, i.e., pentaerythritol (2), is tentatively represented by the symbol Td[Cs], where the Td represents the symmetry of the promolecule and the Cs represents the symmetry of the hydroxymethyl ligand. However, any modes of rotation around the C—C bonds cannot realize the full symmetry of Td so that the pentaerythritol molecule is desymmetrized into D2d at the highest attainable symmetry, as shown by the side-view formula (3).
On the other hand, by replacing each proligand ‘a’ in 1 by a methyl ligand, we obtain tetramethylmethane (2,2-dimethylpropane). The symmetry of the tetramethylmethane (4) is represented by the symbol Td[C3v], because the methyl ligand belongs to C3v-symmetry in isolation. The tetramethylmethane can take the full symmetry of Td at the highest attainable symmetry, as shown by the formula 5.
Figure 1 Models of various levels:
Tetrahedral promolecule with proligands (left),
nonrigid molecule with ligands (center),
and molecule fixed at the highest attainable symmetry (right).
The desymmetrization behaviors due to the symmetries of ligands in isolation (as well as due to the chirality/achirality of proligands) have been systematically discussed on the basis of the subductions of coset representations by Fujita [5, 6]. The previous method by Fujita [5, 6] has adopted a mathematical formulation, where coset representations have been concretely (computationally) obtained by starting from coset decompositions and their subductions have been defined and calculated algebraically by using mark tables [6, 7]. If we can formulate these mathematical concepts in a more intuitive fashion, the Fujita's method [5, 6] will become a versatile tool for comprehending such unexpected phenomena shown in Fig. 1.
In the present paper, coset representations and their subductions reported earlier by Fujita [5, 6] will be reformulated on the basis of a minimum set of group theory, i.e., by using local and global symmetries. This formulation is a substantial extension of the method reported by Fujita [2], so that it will produce more detailed results than those due to the method described in Part I of this series [1]. Thereby, such seemingly unexpected cases as shown in Fig. 1 will be discussed in detail, so that the reader will gain a deeper insight to stereochemistry.
Figure 2 shows various orbits (equivalence classes) that appear in a methane molecule of point group Td, where each orbit contains objects selected variously according to problems to be answered, e.g., atoms (vertices), bonds, edges (hypothetical lines containing two atoms), faces (hypothetical planes containing three or more atoms), bond angles, and any other segments.
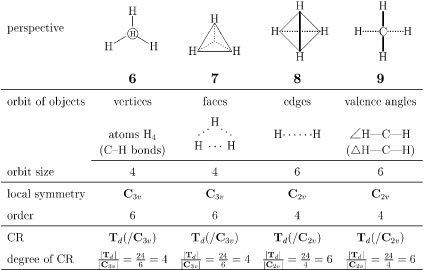
Figure 2 Orbits of various objects in a methane molecule.
Each orbit is characterized by a coset representation (CR) of Td through its local symmetry [8, 9]. The local symmetry of each orbit is determined by fixing any member involved in the orbit. This determination is conducted by an appropriate perspective for fixing the member as follows:
Orbit of hydrogens on vertices. Four hydrogens in a methane molecule are equivalent so as to construct a four-membered orbit. The corresponding coset representation is determined as follows. According to the perspective shown in Fig. 2 (6), the three-fold axis perpendicular to the page through the central carbon atom is found to penetrate the hydrogen depicted by an encircled H, which is immobile (fixed) on the action of every symmetry operation of the relevant point group C3v. The group C3v is called a stabilizer of the orbit, which decides the local symmetry of the orbit. The local symmetry C3v and the global symmetry Td are combined by a coset decomposition, which produces a permutation representation called a coset representation (CR) [10]. For the sake of simplicity, the symbol Td(/C3v) has been coined to designate such a CR [6, 7].
Instead of taking account of the concrete form of the CR Td(/C3v) in the present paper, we can use several features to characterize the orbit. For example, the degree (length) of a CR is generally equal to the size of the corresponding orbit. Thus, the degree of the CR Td(/C3v) is calculated to be |Td|/|C3v| = 24/6 = 4, where |Td| (= 24) and |C3v| (= 6) represent the orders of the respective groups. As a result, we say that the orbit of the four hydrogens is governed (controlled) by the CR Td(/C3v).
The Td-symmetry of a methane molecule (10) is restricted into its subsymmetry by substitution. Let us consider a fluoromethane molecule (11) as such a desymmetrized product, which belongs to C3v (Fig. 3). The above-described objects in the methane molecule (Fig. 2) are influenced by this desymmetrization. Thus, the resulting fluoromethane has orbits of various types as collected in Fig. 4, where respective perspectives are depicted to show the local symmetry of each type of objects. Thereby, the corresponding CRs can be assigned to the orbits appearing in the fluoromethane molecule.
Figure 3
Desymmetrization of methane into fluoromethane.
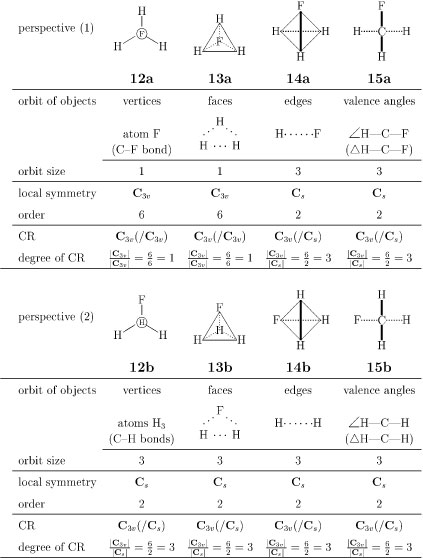
Figure 4
Orbits of various objects in a fluoromethane molecule.
The four hydrogens governed by the CR Td(/C3v) are divided into one fluorine and three hydrogens during the desymmetrization. The fluorine atom in the fluoromethane molecule constructs a one-membered orbit governed by the CR C3v(/C3v), because the F is fixed on the action of C3v as shown in the perspective 12a. On the other hand, the three hydrogen atoms in the fluoromethane molecule construct a three-membered orbit governed by the CR C3v(/Cs), because any one of the hydrogen atoms is fixed on the action of Cs, as shown in the perspective 12b. The desymmetrization process of 6 into 12a and 12b can be represented by the following equation:
| Td(/C3v)↓C3v = C3v(/C3v) + C3v(/Cs), | (1) |
The orbit of the four C—H bonds in the methane molecule, which is governed by the CR Td(/C3v), obeys the same subduction as represented by eq. 1. The desymmetrization process of the four H-H-H faces (7) into one H-H-H face (13a) and three H-H-F faces (13b) can be also represented by eq. 1.
The orbit of the six hypothetical edges (H…H) in the methane molecule (cf. 8), which is governed by the CR Td(/C2v), is desymmetrized into C3v, where the orbit is divided into a three-membered orbit of H…F edges (the perspective 14a) and a three-membered orbit of H…H edges (the perspective 14b). By considering the local symmetries derived from these perspectives, both of the orbits are determined to be governed by the CR C3v(/Cs). Hence, the desymmetrization process of 8 into 14a and 14b can be represented by the following subduction:
| Td(/C2v)↓C3v = 2C3v(/Cs). | (2) |
By considering the original perspective (9) and the resulting perspectives (15a and 15b), we can conclude that the six-membered orbit of the six H—C—H angles (∠ H—C—H) is desymmetrized according to eq. 2 and that the six-membered orbit of the six planes (ΔH—C—H) is desymmetrized according to eq. 2.
The subductions of CRs can be systematically obtained by an algebraic method developed by Fujita [6, 11] and have been reported in tabular forms named subduction tables. The concrete form of the subduction table for Td has been reported in a previous article [12] and a book [6]. It should be noted that such subduction tables are obtained algebraically, i.e., irrespective of objects to be examined. In other words, they are applicable to any orbits of any objects, so long as they match symmetries concerning the objects. Although the present paper does not deal with the subduction tables, such tables as collected in Ref. [6] should be referred to if the full lists of subductions are required.
As clarified in the preceding discussions, the desymmetrization (Fig. 3) of methane (Td) into fluoromethane (C3v) can be characterized by the desymmetrization of the relevant orbits. Thus, the orbits shown in Fig. 2 for the methane molecule are converted into the orbits shown in Fig. 4 for the fluoromethane molecule. The desymmetrization of such an orbit is controlled by a subduction (e.g., eq. 1 and eq. 2) that is obtained algebraically. It should be emphasized that the subduction represented by eq. 1 and that represented by eq. 2 are concurrent during the desymmetrization process from Td to C3v.
On the same line, each of the subgroups of Td appears during the desymmetrization. The results are collected as a group/subgroup lattice (Fig. 5), which contains the data of subductions with respect to vertices and edges. In Fig. 5, each molecule is depicted in a promolecule level as a result of vertex desymmetrization so that a D2d- or D2-molecule does not appear, as shown by a vacant frame.
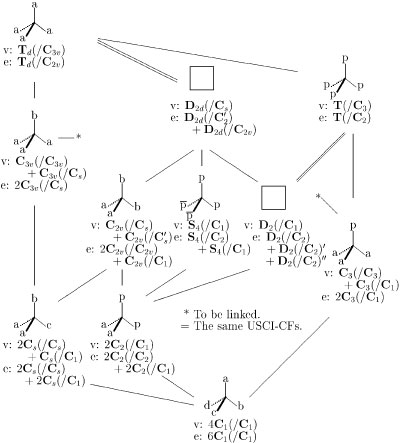
Figure 5
Desymmetrization of orbits in a tetrahedral molecule,
where subduction data are designated as
v: vertex desymmetrization and e: edge desymmetrization.
The letters a, b, c, and d represent atoms or achiral proligands,
while the letters p and
represent
an enantiomeric pair of chiral proligands.
The term ``proligand'' is defined
as a hypothetical structureless object that has chirality/achirality.
The resulting promolecules are depicted according to
a vertex desymmetrization.
It is worthwhile to describe the relationship between the USCI-CF method (Part I of this series [1]) and the present method (Part II). Let G be a point group and H be its subgroup. Then, the coset representation G(/H) obtained as above is classified into one of the three sphericities so that it is ascribed to a sphericity index as follows [6, 12]:
| G | H | G(/H) | sphericity index |
| achiral | achiral | homospheric | a|G|/|H| |
| achiral | chiral | enantiospheric | c|G|/|H| |
| chiral | chiral | hemispheric | b|G|/|H| |
Because a coset representation corresponds to a sphericity index and because a sum of coset representations generated by a subduction of a coset representation corresponds to a USCI-CF, the concurrent desymmetrizations of orbits discussed by USCI-CFs in Part I [1] can be also discussed by means of the subduction. This means that the subduction data (along with the USCI-CF data) are useful to judge the equivalency of tetrahedral models of different types, which was discussed otherwise by Lloyd-Williams and Giralt [4]
When sphericities in the form of USCI-CFs are used as a probe to test desymmetrization, the chirality/achirality of a proligand is taken into consideration. On the other hand, when coset representations in the form of subduction data are used as a probe to test desymmetrization, the symmetry (local symmetry) of a ligand is taken into consideration. The latter fact rationalizes the phenomena shown in Fig. 1.
Let us again consider the two cases shown in Fig. 1 in terms of CRs, where matched and mismatched molecules are a key concept to discuss the difference between the two cases [5, 6].
Let us consider why pentaerythritol (3) is restricted to belong to D2d-symmetry (cf. Fig. 1). In order that pentaerythritol (3) belongs to Td, the symmetry of a hydroxymethyl ligand (Cs) should be matched to the local symmetry (C3v) of the corresponding CR Td(/C3v). Obviously, this condition is not satisfied. The ligand symmetry becomes matched to the local symmetry if the CR D2d(/Cs) is adopted. Thereby, 3 is ascribed to D2d, which is equal to the highest attainable symmetry.
As for 5 (Td), on the other hand, the symmetry of a methyl ligand (C3v) is matched to the local symmetry of the corresponding CR Td(/C3v). Hence, 4 is ascribed to Td, which is equal to the highest attainable symmetry.
On the same line as the two cases shown in Fig. 1, matched and mismatched molecules can be found for T-symmetry and D2-symmetry. The following exercises challenge the reader to comprehend the importance of local symmetries appearing in CRs .
Exercise 1: Consider a molecule belonging to D2-symmetry by examining the data shown in Fig. 5, where each chiral proligand (p) of Cp4 is replaced by an R-CXYZ ligand of C1-symmetry. Discuss a method of maintaining the T-symmetry of the Cp4-promolecule. See Refs. [13] and [14] for synthetic examples. See also [15] for a discussion on their symmetries, which has been different from the present approach.
Exercise 2: Suppose that each of the two achiral proligands (a) of the Ca2p2-promolecule (Fig. 5) is replaced by a chiral proligand (q) different from the p. Explain that the resulting promolecule Cp2q2 belongs to the same point group C2 as the Ca2p2-promolecule.
Exercise 3:
Consider that a Cabp
or Cbcp
-promolecule belongs
to Cs-symmetry.
Compare this promolecule with the Ca2bc-promolecule
of Cs-symmetry
by using the subduction data shown
below the latter formula (Fig. 5).
Exercise 4:
Consider a molecule belonging to S4-symmetry
by examining the data shown in Fig. 5,
where each chiral proligand (p) and its enantiomeric ligand
(
)
in the Cp2
2-molecule
are replaced by an R-CXYZ and an S-CXYZ respectively.
Show that the two p's and the two
's are equivalent
so as to construct a four-membered enantiomeric orbit.
Subductions of coset representations are examined manually by considering the local symmetries of orbits of objects, e.g., atoms (vertices), bonds, edges (hypothetical lines containing two atoms), faces (hypothetical planes containing three or more atoms), bond angles, and any other segments. Since the subduction data obtained manually are equivalent to those derived algebraically, the former data can be effectively used in the methods that have been developed previously for the latter algebraically-obtained subduction data. The merit of the manual derivation has been examined by tasks for finding molecules matched and mismatched to local symmetries. Thereby, the manual derivation of subduction data is proved to be a novel way for understanding the desymmetrization of the tetrahedron in introductory courses of organic stereochemistry.
Top
CEJ Vol. 8, No. 2, Contents