Chemical Education Journal (CEJ),
Vol. 13, No. 2 /Registration No. 13-15 /Received June 27, 2009.
URL =
http://chem.sci.utsunomiya-u.ac.jp/cejrnlE.html
Abstract
A visual description of finding characters of irreducible
representation (CIR) of the D6h point group
is given. A similar approach has been earlier discussed for the
D3h group in CEJ. The method applied is
based on transformations of the plane figure, a counterpart to
a given molecule by the operations of its symmetry, because to
both (the figure and the molecule) with the same operations are
assigned. The present model visualizes the approach applied by
The Group Theory and gives the same results.
Contents
A. Symbols of different vibration symmetry types and kinds of figures
B. Figures and the way of their transformations
In spectroscopy1 the molecule and the symmetry of its vibrations play very important role. Molecules of the same symmetry have similar spectra. There is a field of mathematics called Group Theory which enables a description of molecules and their vibrations according to their symmetry. Vibrations performed by the molecules (we usually take into account the so-called normal vibrations2) reflect their spatial shape and the Group Theory offers a possibility to determine which of them are active (observable) in infrared (IR), Raman and hyper-Raman spectra. The spectra provide much information on the molecules, e.g. on their structure, the type and the strength of bonds, the density of the electric charge distribution and a possible dipole and/or higher multipole moments. This information permits prediction of the chemical reactivity. The symmetry allows us to answer the question of what types of vibrations the molecule performs and how many of them are manifested in the spectrum. But instead of exploring directly the molecule we focus on the geometrical figure which has the same symmetry operations. Next, we will perform the figure's transformations through the symmetry operations. The results will allow us to obtain CIR and determine the number of vibrations and their types. The method has been earlier applied for the C2v, C4v and D3h point groups.3,5 In this article we show how to expand the visual approach of obtaining CIR for the D6h point group. The approach is simple in its application and gives almost immediate results. Thereby, it can be applied for introductory molecular chemistry (physics) classes. In addition, there are computer simulations (animations) and software which refer to the D6h group.4 The simulations illustrate the oscillations of benzene (it belongs to the D6h group) and transformations of a chosen geometrical figure through all symmetry operations assigned to it. We observe results of transformations which allow us to find CIR. Symmetry operations and CIR serve also as data for the software which enables us to get the number and the symmetry type of given oscillations.
The paper is organized as follows:
Section II presents the types of figures in relation to the types
of
vibrations and describes the way of finding CIR on the basis
of transformations of geometrical figures.
Section III gives a mathematical insight into the method applied.
II. CHARACTERS OF IRREDUCIBLE REPRESENTATIONS OF THE D6h GROUP
Symmetry operations5 of a molecule create a point group and correspond to a matrix. Such a matrix shows the way the coordinates of a point get transformed in an operation considered. We can choose, for example, one of the molecule's atoms (except the central atom) as a point of reference for transformations. Transformation matrices are one of possible representations of a point group. The essential quantity in the Theory of Representations is the character. It is the sum of diagonal elements of a given matrix. The character enables us to determine the number and the type of vibrations which a given molecule performs. The method applied in this work is based on transformations of a figure which has the same symmetry operations as the molecule considered. Here we consider a hexagon. We divide the figure into parts but its outline remains unchangeable. To this parts we assign the signs (+) and (-). If, as a result of transformation of the figure which represents non-degenerate vibrations, we obtain unchanged figure, then to the result of this transformation the value 1 is assigned. On the other hand, when the signs change, e.g. (+) is exchanged for (-) and vice versa, then the value -1 is assigned to the result of the transformation.
In the case of figures which represent degenerate vibrations we use sets of numbers given by Eq.(1-4). In addition, in this case as well, signs plus and minus may appear in the front of a figure as well as on its back (see Fig. 1).
A. Symbols of different vibration symmetry types and kinds of figures
An exemplary molecule belonging to the D6h group is that of benzene. Its shape corresponds to a hexagon and therefore we take for our transformations this figure. Each vibration symmetry type refers to one figure. The figure's outline may be divided into parts and to each part the sign (+) or (-) is assigned. The way of the division and the arrangement of signs is related to the symbols and indexes which serve to identify the type of symmetry. In order to define the symbols and indexes, the designation Òsymmetric figureÓ and Òantisymmetric figureÓ is used. The symmetric figure means that the signs of the figure after transformation are unchanged. In the antisymmetric figure signs are exchanged i.e. (+) changes into (-) and vice versa. In general we use the standard notation for molecular vibrations. We briefly describe their meaning:
(i) The symbol (A, B) - A denotes symmetric and B antisymmetric vibrations with respect to the highest multiplicity axis. The figures of type A are symmetrical with respect to the rotation by 180° (we make this rotation with respect to the highest multiplicity axis), whereas the figures of type B are antisymmetric with respect to the same axis of rotation. It means that the result of the rotation of the type A figure gives the figure unchanged and the result of the rotation of the type B figure gives the figure with the opposite signs (the place marked by (+) changes into (-) and vice versa).
(ii) The symbol (E) denotes double degenerate vibrations. It leads to the necessity of considering two groups of figures.
(iii) Index (g, u) - index g denotes symmetricity and u antisymmetricity of a vibration with respect to the molecule's center of symmetry. Index g, with reference to a figure, means that the figure must have such a form that one gets the same figure after performing the inversion with respect to the figure's centre. Index u defines a figure that yields the opposite figure when again the operation of inversion is performed. For example, the inversion of the figure within B1g yields the same figure because of g symmetry (see Fig. 1(h)), whereas the figure within B2u is antisymmetrical with respect to inversion leading to exchange of signs because of u symmetry (Fig. 1(g)). For figures that deal with the degenerate vibrations we take two figures, the so-called Introductory Figures (IF) (see section II(B)) and perform the transformation. Each of the IF leads separately to the special way of attributing numerical values to transformations considered.
(iv) Index (1, 2) - index 1 denotes symmetricity and 2 antisymmetricity of a vibration with respect to the axis other than the highest multiplicity one. First, we will consider figures which refer to nondegenerate vibrations. For such figures the transformation corresponding to the axis other than the highest multiplicity one is the C2 rotation with respect to the axis passing through the midpoints of the hexagon's opposite sides or with respect to the axis passing through the opposite vertices of the hexagon. The choice of one out of the two axes is arbitrary. The way of utilizing indexes (1, 2) is different for A and B types of figures.
For type A - index 1 means that the figure obtained is the same as the initial one (after performing transformation of the initial figure), whereas index 2 (for the same type) means that the figure obtained is the opposite of the initial one (the signs are exchanged, i.e. (+) changes into (-) and vice versa).
For type vibration of the type B - the effects of transformations are exactly the opposite to the ones for type A.
For degenerate vibrations and figures which correspond to the vibrations, the principle of indexing (1, 2) is as follows: we consider rotations by the odd multiplicities of 60°, i.e. 60°, 180° and 300° with respect to the highest multiplicity axis. The angles of rotations refer to the operations C6, S6, C2, C65, S65.
Index 1 means that if the Introductory Figure is rotated by 60° (C6, S6) or by 300° (C65, S65), then neither of the operations change the number's sign assigned to IF, and change the sign into opposite one if IF is rotated by 180° (C2). Index 2 informs that if IF is rotated through the same operations as for the 1 case, then the results are opposite to the ones obtained for 1, or there is no change of the number's sign assigned to IF for the operation C2 and change of the sign for C6, S6, C65, S65.
We emphasize that the number's sign is discussed here but not the number's value.
B. Figures and the way of their transformations
Let us consider the figures used to obtain CIR of non-degenerate vibrations, Fig. 1. They can have the same signs on both the planes (the front-plane sign is the same as the back-plane one, Fig. 1(a),(c),(e),(g)) or the opposite signs on the two planes, (Fig. 1(b),(d),(f),(h)). If we transform a chosen figure and obtain unchanged one then the numerical result equal to 1 is assigned to this transformation, however if after the transformation the signs are exchanged, namely (+) changes into (-) and vice versa, then we assign the value -1 to this transformation.
| (a) |  |
(c) | 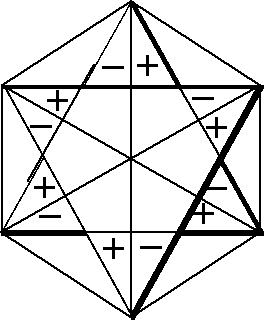 |
| (b) | 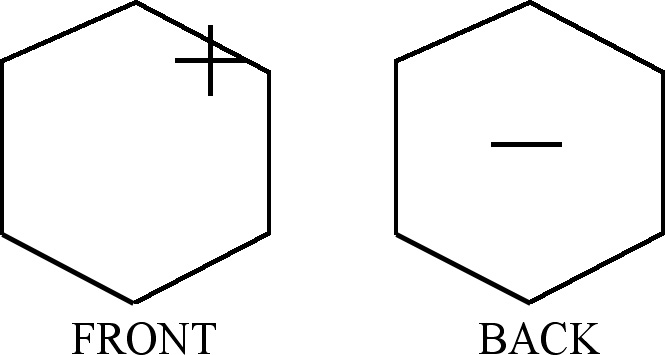 |
(d) | 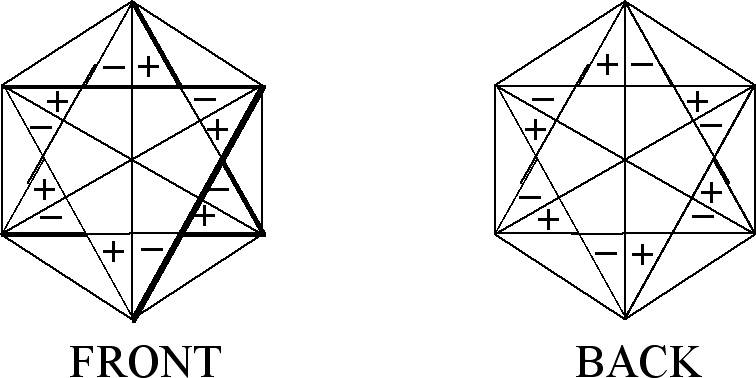 |
| (e) | 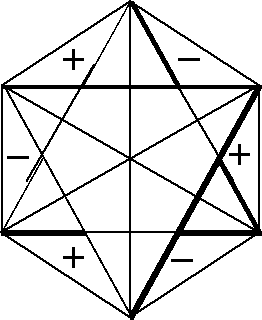 |
(g) | 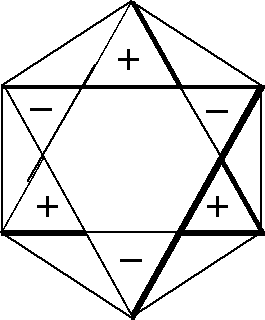 |
| (f) | 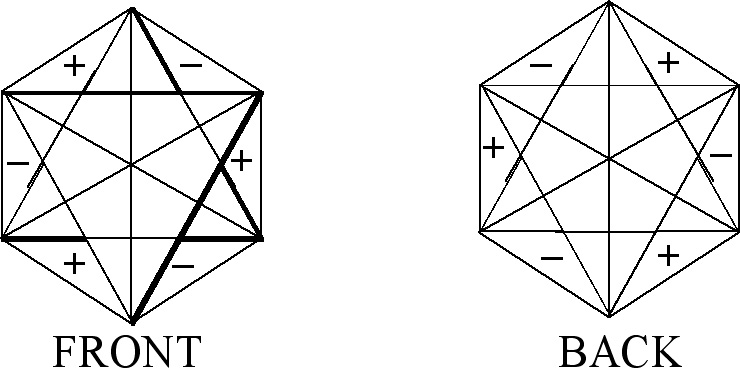 |
(h) | 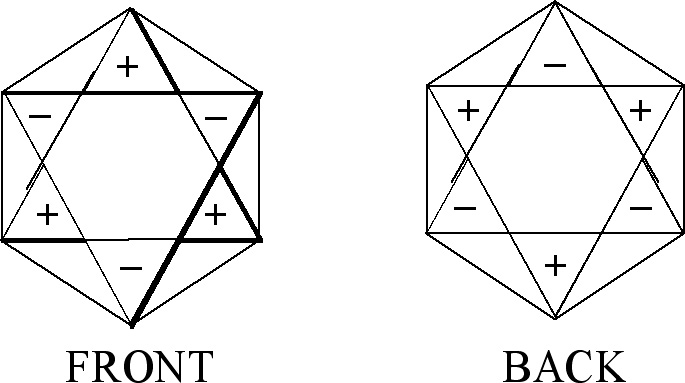 |
Fig. 1. Figures used to obtain CIR of non-degenerate vibrations
(a) The figure leading the characters of A1g
symmetry type
(b) The same figure as in (a) but with the opposite signs on both
sides of its plane. The figure permits getting the characters
of A2u
(c) This figure is used to obtain the characters of A2g
symmetry type
(d) The same figure as in (c) but with the opposite signs on both
sides of its plane, it permits getting A1u
(e) The figure for finding the characters of B1u
symmetry type
(f) The same figure as in (e) but with the opposite signs on both
sides of its plane. It permits getting the characters corresponding
to B2g
(g) The figure enables getting the characters of B2u
symmetry type
(h) The same figure as in (g) but with the opposite signs on both
sides of its plane. It permits getting the characters of B1g
Now, let us analyze the degenerate vibrations. In order to get CIR which correspond to these vibrations we make use of the figures discussed below. The figures that enable us to obtain the characters of E1u and E1g symmetry types are presented in Fig. 2.
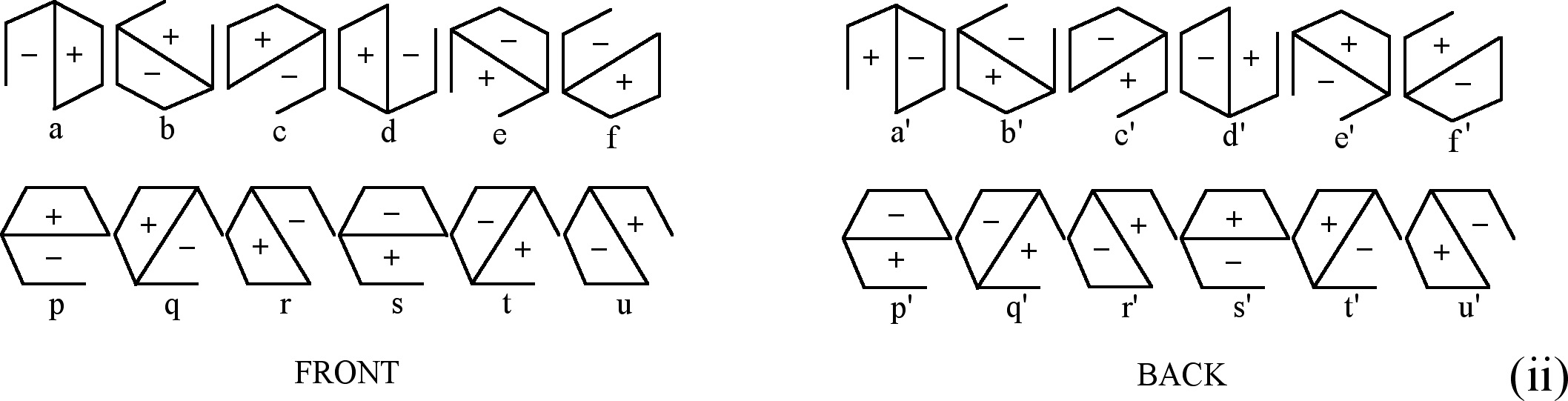
Fig. 2. Figures used to obtain CIR of E1u type (i) and E1g type (ii)
There are two groups of figures (a, b, c, d, e, f) and (p,
q, r, s, t, u) that can be used to obtain CIR of E1u
type (see Fig. 2 (i)). Each
figure (hexagon) in a given group is rotated with respect to the
previous one by 30° in the counterclockwise direction. Each
hexagon is divided into two parts and to each part a sign is assigned.
The two signs are the opposite. The front-plane sign is the same
as the back-plane one. The procedure to obtain CIR is as follows:
we choose one hexagon from each group, for example a and
p are the so-called Introductory Figures (IF), and make
transformation according to D6h symmetry
operations. If one obtains IF after the conversion then the numerical
value equal to 1 is assigned, whereas if one obtains the opposite
figure to IF then we assign value -1 to the result. For instance,
the opposite figure to a is d, and the opposite
to p is s. When the resultant figure (the final
figure) is rotated with respect to IF by 60û and 300û
then to the result of this transformation the numerical value
1/2 is assigned and for the opposite case the numerical value
equal to -1/2 is assigned, so if IF are a and p
then:
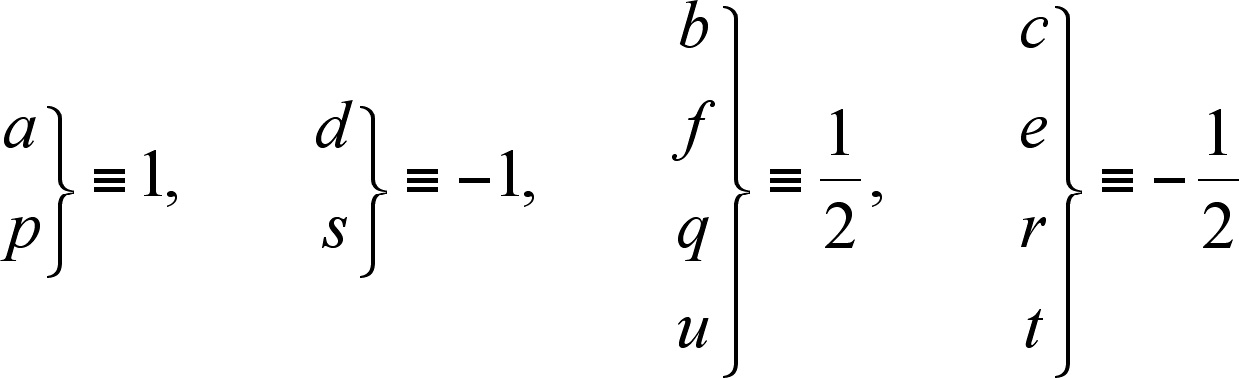 (1)
(1)
The hexagons appear in pair composed of two figures namely
the hexagon from the first group is located on top of hexagon
from the second group (see Fig. 2).
It means that it is possible to choose (a, p) or (c,
r) but not e.g. (a, t). It should be remembered
that if we make the transformations with respect to the diagonal
axis of the hexagon which belongs to the first group then the
transformations of the second group must be made with respect
to the same axis.
There are two numbers which result from the transformation of
a figure from the first group and from the second group, respectively.
We add together these two numerical results and we get CIR.
For 3C2', 3C2",
3s(Gk. sigma)d,
3 sv one finds
the characters in the following way. Three transformations are
performed for each axis defining operation C2'
and three for the operation C2", as
well as three transformations for each plane of sd symmetry and three for sv one. Let us consider, for example, the operation
C2', and then the first group chosen figure
and the second group one are rotated with respect to the three
axes of symmetry --each figure separately. The result of each
of the three transformations (in one group) is the number given
by Eq. (1). So, there are three numbers for one group.
The three found numbers are added up to get the numerical
result of the transformations for the first group of hexagons.
Analogous procedure is carried out for the second group.
Finally, we add up the two numbers found (numerical results
for the two groups) obtaining CIR for a given symmetry operation.
In order to get CIR of E1g symmetry
type we make use of figures shown in Fig. 2(ii). They are the
same figures as for E1u but with
the opposite signs on the front and back plane of a figure. The
assignment of the numbers is the same as in E1u.
If we choose (a, p) as IF, then:
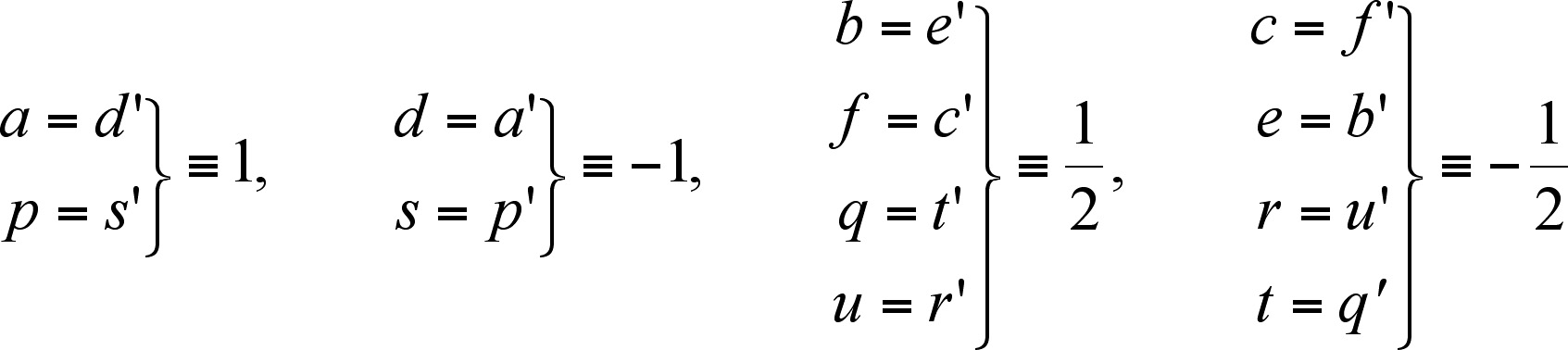 (2)
(2)
The procedure for obtaining CIR is the same as for E1u.
The last two symmetry types and their characters can be found
on the basis of the figures shown in Fig.
3.
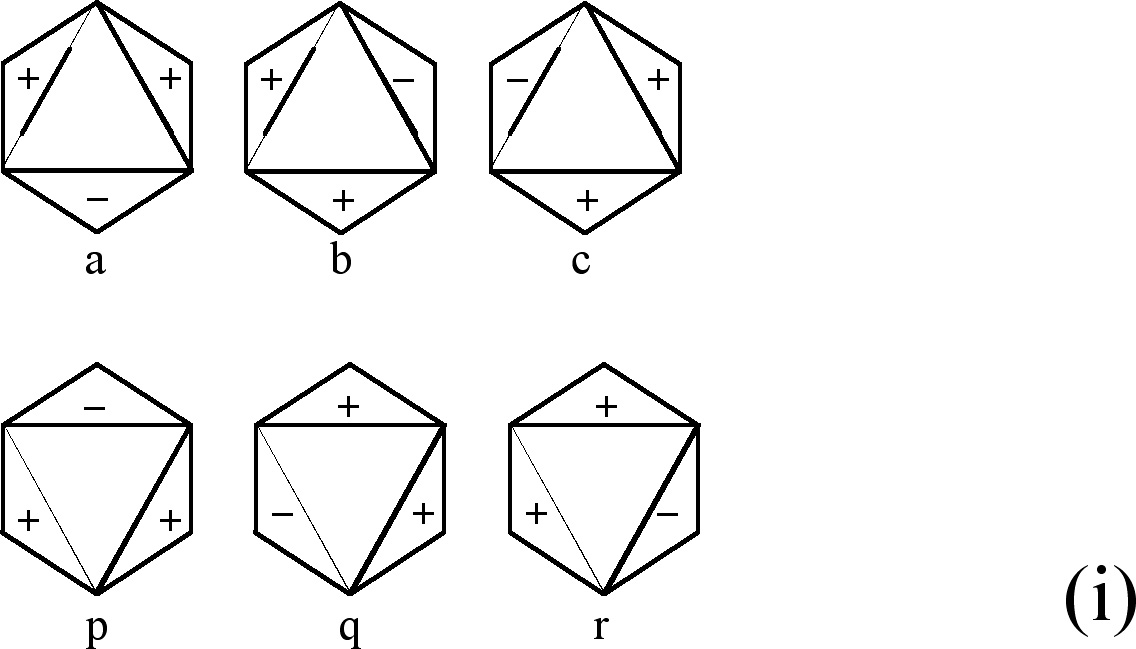
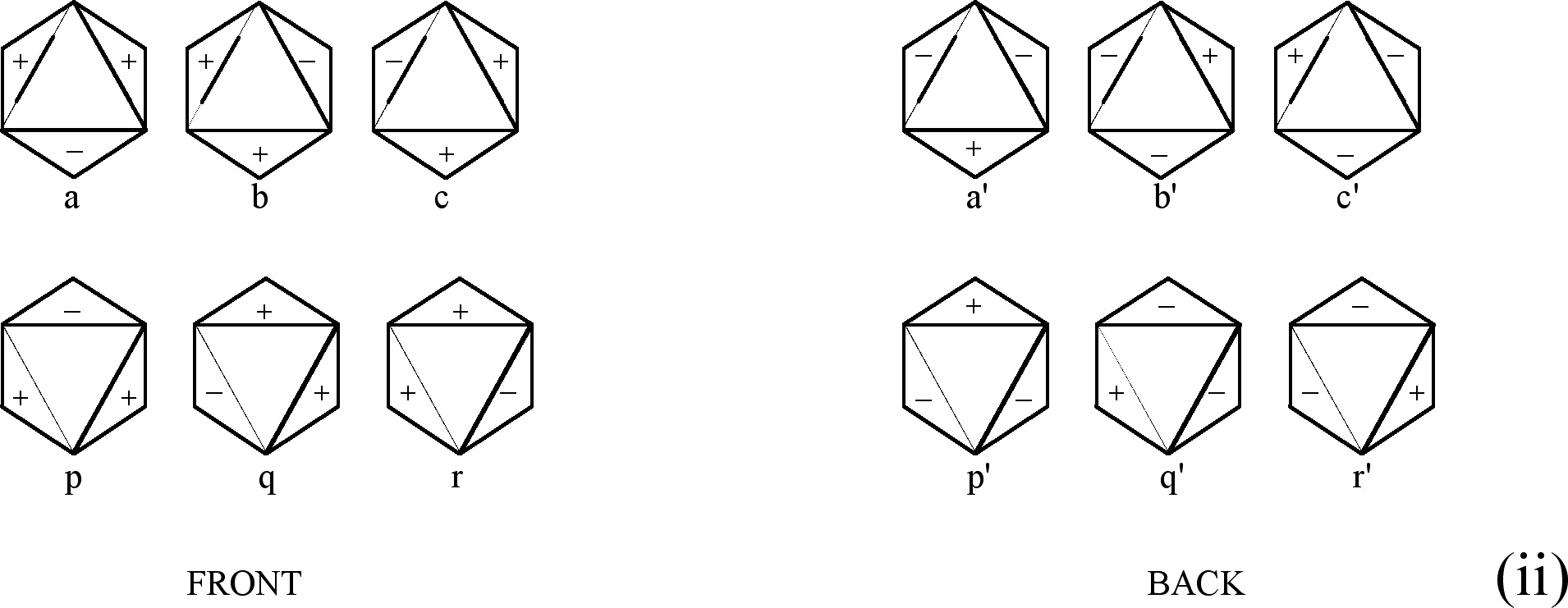
Fig.3. The above figures permit getting CIR of (i) E2g
and (ii) E2u types
Let us consider figures corresponding to E2g. We have two groups of figures (a, b, c) and (p, q, r) -- see Fig. 3(i). In each group the subsequent figure has the signs rotated with respect to the previous one by 120û. The group (p, q, r) can be obtained by defining the (a, b, c) group. For example, we can take a from the first group and reflect it with respect to the horizontal plane which is parallel to the bottom side of the triangle inscribed inside the hexagon a. We get the figure p by this operation. The other members of the figures of the second group are obtained by 120° and 240° rotation of the figure p, respectively. Another procedure is to transform b with respect to the plane parallel to the right side of the triangle to get q or transform c with respect to the plane parallel to the left side of the triangle to get r. The remaining figures are obtained by 120° and 240° rotation of the first one. The assignment of numbers as follows:
![]() (3)
(3)
The procedure of transformations is the same as for E1u and E1g.
Fig. 3(ii) presents the same figures as in E2g
but with the opposite signs on both sides of the plane which distinguish
the front and the back of the figures. The numbers assigned to
the figures are the same as in E2g,
except for those which correspond to the so-called primed ( '
) figures. For these figures the opposite numbers are assigned
(see (4)). The way of the transformations of the figures corresponding
to E2u is the same as for E1u, E1g and
E2g
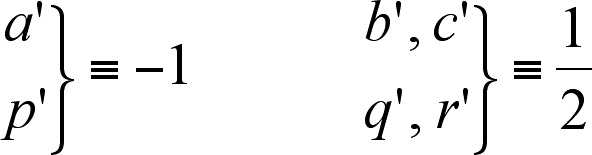 |
(4) |
The symmetry operations of a molecule belonging to the D6h
group can be described in terms of matrices. Let us assume that
the molecule lies on XY plane, then the matrices are given by
expressions (6).
The superscripts ( ' ) and ( " ) (see matrices (6)) refer
to the rotation with respect to the axis passing through the opposite
sides of the hexagon and the diagonal axis, respectively. The
matrix elements are found according to the literature-known methods
with slight modifications for C2' and C2", for which the angles used to calculate
the matrices are as follows:
For ( ' ) the angles satisfy the expression:
180o + (2n + 1) · 60o, "n"
is an integer. E.g.
n = 0, then 180o + (2 x 0 + 1) x 60o = 240o,
which refers to M(C2 + 6),
n = 1, then 180o + (2 x 1 + 1) x 60o = 360o,
--> M(C2 + 3 x 6),
n = 2, then 180o + (2 x 2 + 1) x 60o = 480o,
--> M(C2 + 5 x 6).
For ( " ) the angles satisfy the expression:
180o + 2n x 60o,
n = 0, then 180o + 2 x 0 x 60o = 180o,
which refers to M(C2),
n = 1, then 180o + 2 x 1 x 60o = 300o,
--> M(C2 + 2 x 6),
n = 2, then 180o + 2 x 2 x 60o = 420o,
--> M(C2 + 4 x 6).
The usage of other " n" doesn't change the value
of the sine and the cosine because of their periodicity (see the
rotation matrix (5)).
![]()
For 3sd and
3sv the same
numbers appear on the main diagonal of their matrices as for 3C2' and 3C2".
The numbers on the main diagonal are the same as those found as
a result of the E1u figures transformation
process (see (1)).
On the other hand, for A1g the determinants
of the matrices (5) are calculated to get the characters.
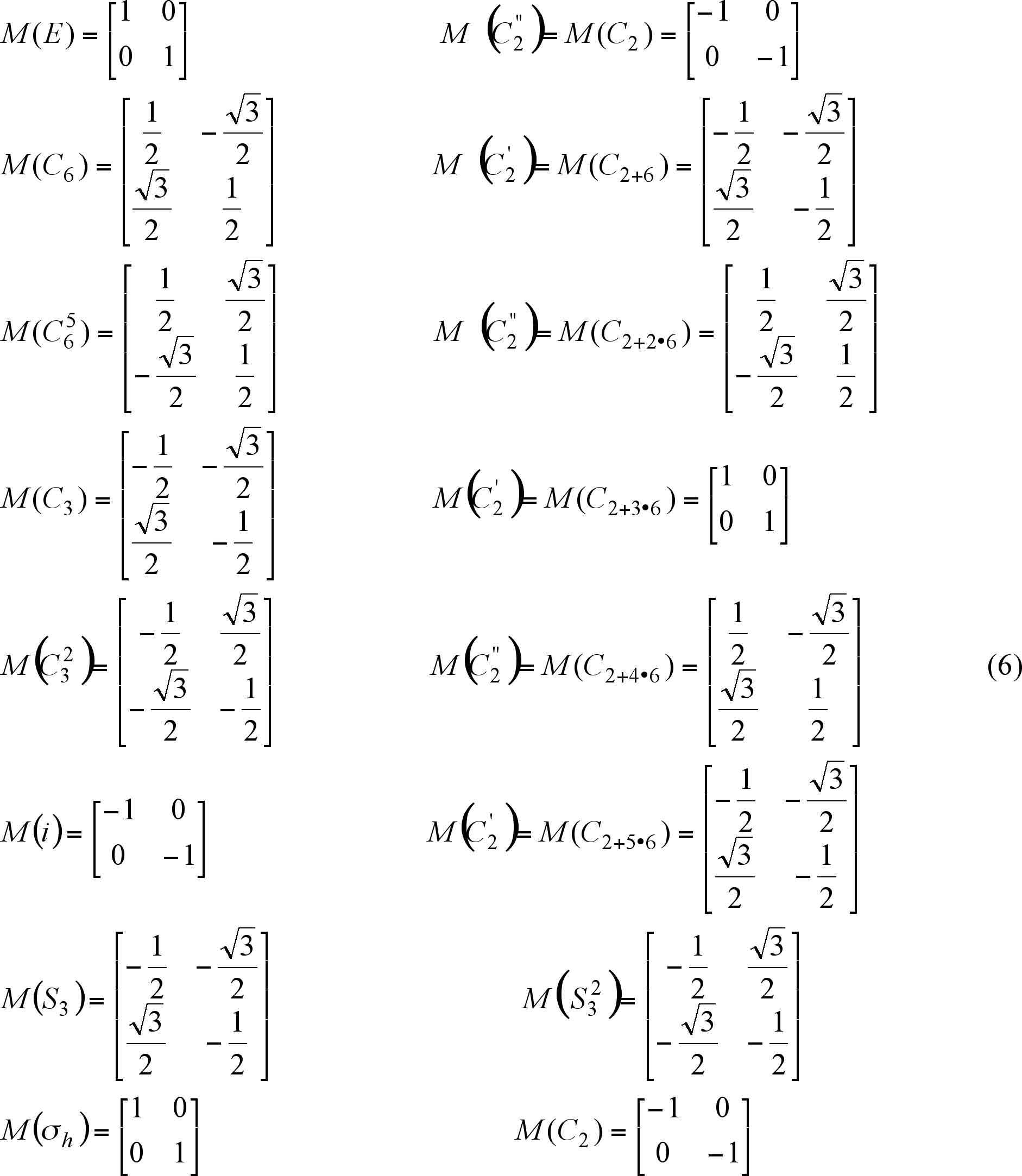
Detailed depiction of interrelation between matrices and numbers assigned to the results of the transformations, for degenerate vibrations, can be found in the appendix.
This paper presents a visual method of obtaining characters for all the D6h group irreducible representations. Similar method has been previously applied for the D3h group. The model is based on taking advantage of the figure (figures) corresponding to a given type of symmetry and its (their) transformations through all symmetry operations which are assigned to an examined molecule. In order to make use of such a possibility one needs to notice interrelation between symbols and indices which depict the symmetry type and the form of the corresponding figure. By this means, we have an opportunity to find CIR in visual and transparent way, which makes the model clear and applicable even for introductory courses of physics and chemistry. What's more, the method has been supported by a number of computer simulations and a software, giving the readers a chance to explore the discussed topic by him -- or herself. The mathematical insight (see sec.III) -- based on results of Group Theory6 -- proves the correctness of the model. The model is not associated with one point group only but can applicable for other point groups, too.
This paper in part has been supported by the Ministry of Education, Poland, Grant Nb. N 202069933.
1) Gordon M. Barrow, Introduction
to Molecular Spectroscopy, (McGraw-Hill, New York, 1962).
2) M. Hollas, Basic Atomic and Molecular
Spectroscopy, (Royal Society of Chemistry, 2002).
3) T. Bancewicz, A. Kaminski, The
geometrical model for obtaining the D3h group's characters of
irreducible representations and symmetry types, Chem. Educ.
J. 12, No. 1, (2009).
4) Computer simulations and software
are available at < www.matphys.kki.pl>.
You have to write down the address in the field of addresses of
www page. Don't write down it in other fields, for example "Google".
5) P. Kowalczyk, Fizyka cz_steczek
(Physics of Molecules), (PWN SA, Warsaw, 2000), Chap.1, p.12.
and pp.35 - 44.
6) J. F. Cornwell, Group Theory in
Physics, (Academic Press, London, 1984).
Recommended literature
H. Haken and H. C. Wolf, Molecular Physics with Elements of
Quantum Chemistry, (PWN SA, Warsaw, 1998).
R. L. Carter, Molecular Symmetry and Group Theory, (J. Wiley and
Sons, N.York, 1997).
J. F. Cornwell, Group Theory in Physics, (Academic Press, London,
1984).
D.R. Lide, Handbook of Chemistry and Physics, (CRC Press, London,
N.York, Washington 2004).
Z. Kecki, Elementy Spektroskopii Molekularnej (Elements of Molecular
Spectroscopy), (PWN, SA, Warsaw, 1998).
L. Landau and E. Lifszyc, Quantum Mechanics, (PWN, Warsaw, 1958).
I. W. Sawieliew, Physics Lectures, (PWN, Warsaw, 1998).
R. Liboff, Introduction to Quantum Mechanics, (PWN, Warsaw, 1987).